Bài 6. Định luật Boyle. Định luật Charles

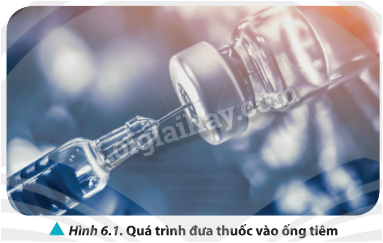
Để đưa thuốc từ lọ vào trong xilanh của ống tiêm, ban đầu nhân viên y tế đẩy pit- tông sát đầu trên của xilanh, sau đó đưa đầu kim tiêm (được gắn với ống tiêm) vào trong lọ thuốc. Khi kéo pit-tông, thuốc sẽ chảy vào trong xilanh (Hình 6.1). Quá trình lấy máu dùng trong xét nghiệm tại các cơ sở y tế cũng hoàn toàn tương tự. Ứng dụng trên dựa vào các định luật của chất khí. Vậy, đó là những định luật nào?

1. Dự đoán mỗi liên hệ giữa áp suất và thể tích khi nén pit-tông xuông hoặc kéo pit-tông lên.

2. Tiến hành thí nghiệm theo các bước hướng dẫn, từ đó tính toán và kiểm tra biểu thức dự đoán, rút ra kết luận về mối liên hệ giữa p và V

1. Từ số liệu Bảng 6.1, vẽ đồ thị biểu diễn mối liên hệ giữa p và V trong hệ toa độ p - V và p - \(\dfrac{1}{V}\). Nhận xét về dạng đồ thị.

2. Từ Hình 6.4, chứng minh rằng: T2 > T1

Nén đẳng nhiệt một khối khí từ thể tích ban đầu 9 lít xuống còn 4 lít. Áp suất của khối khí sau khi nén tăng hay giảm bao nhiêu lần?

Dựa vào định luật Boyle, giải thích tại sao có thể rút thuốc (thể lỏng) từ trong lọ thuốc vào xilanh của ống tiêm khi nhân viên y tế kéo pit-tông như Hình 6.1.

Tiến hành thí nghiệm theo các bước hướng dẫn, thu thập số liệu T, V trong các lần đo. Từ đó:

- Vẽ đồ thị V theo T trong hệ trục toạ độ V - T, nhận xét dạng đồ thị.

- Rút ra mối liên hệ giữa V và T trong quá trình biến đổi đẳng áp.

Dựa vào thuyết động học phân tử chất khí, hãy giải thích vì sao đường đẳng áp p2 lại ở trên đường đẳng áp p1 trong hình 6.7

Cho một khối khí dẫn nở đẳng áp từ nhiệt độ t1 = 32 °C đến nhiệt độ t2 = 117 °C, thể tích khối khí tăng thêm 1,7 lít. Xác định thể tích khối khí trước và sau khi dãn nở.

Hình nào dưới đây mô tả quá trình đẳng áp của một khối lượng khí xác định?

Một khối khí xác định dãn nở đẳng nhiệt từ thể tích ban đầu 5 lít đến 12 lít thì áp suất khối khí đã giảm một lượng 80 kPa. Áp suất ban đầu của khối khí bằng bao nhiêu?

Một mô hình áp kế khí (Hình 6P.1) gồm một bình cầu thủy tinh có thể tích 270 cm3 gắn với một ống nhỏ AB nằm ngang có tiết diện 0,1 cm2. Trong ống có một giọt thủy ngân. Ở 0 °C giọt thủy ngân cách A 30 cm. Tính khoảng di chuyển của giọt thủy ngân khi hơ nóng bình cầu đến 10 °C. Coi thể tích bình là không đổi.

Vào những ngày trời nắng nóng, nhiệt độ không khí ngoài sân là 42 °C, trong khi nhiệt độ không khí trong nhà là 27 °C. Xem áp suất không khí trong nhà và ngoài sân là như nhau. Khối lượng riêng của không khí trong nhà lớn hơn khối lượng riêng của không khí ngoài sân bao nhiêu lần?