Bài 15: Năng lượng liên kết hạt nhân

Trang 100

Mở đầu

100

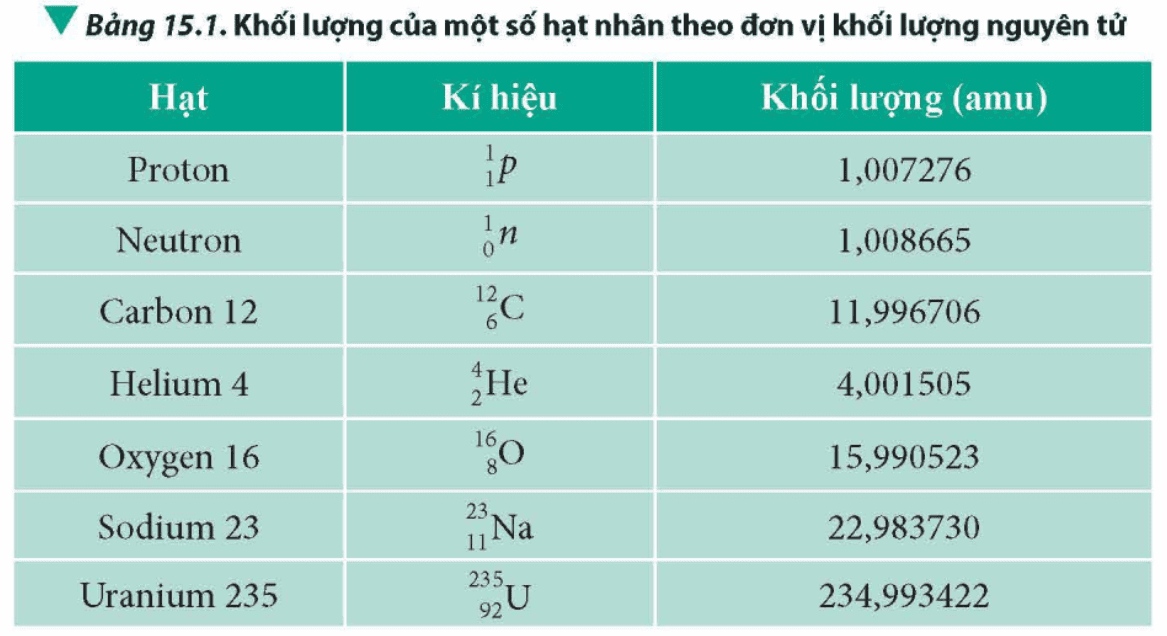
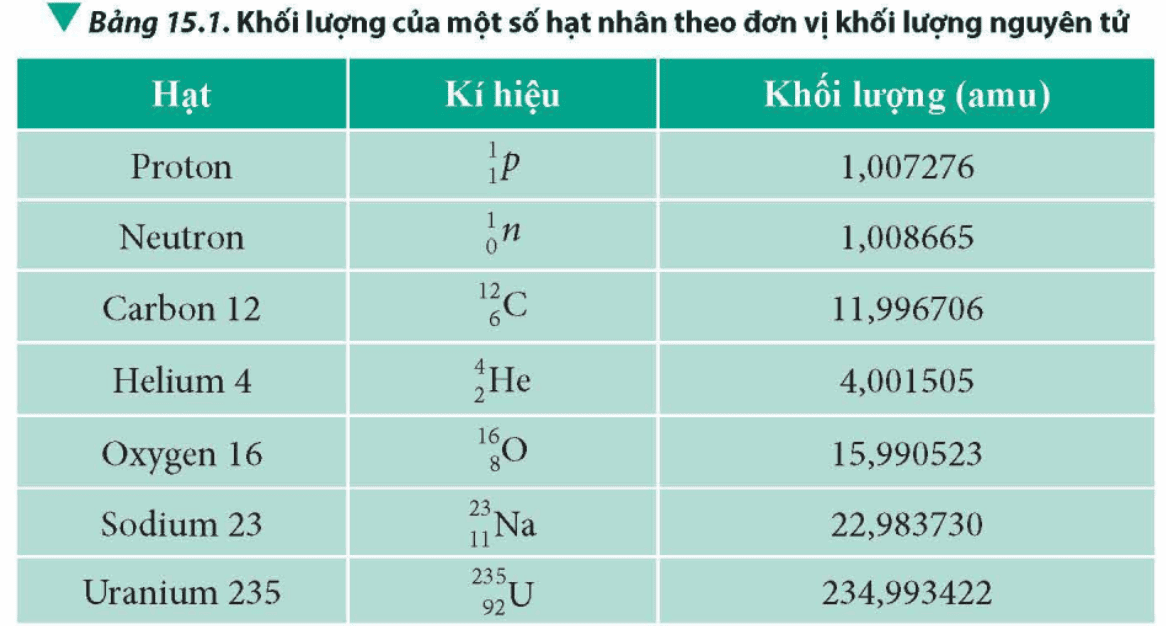
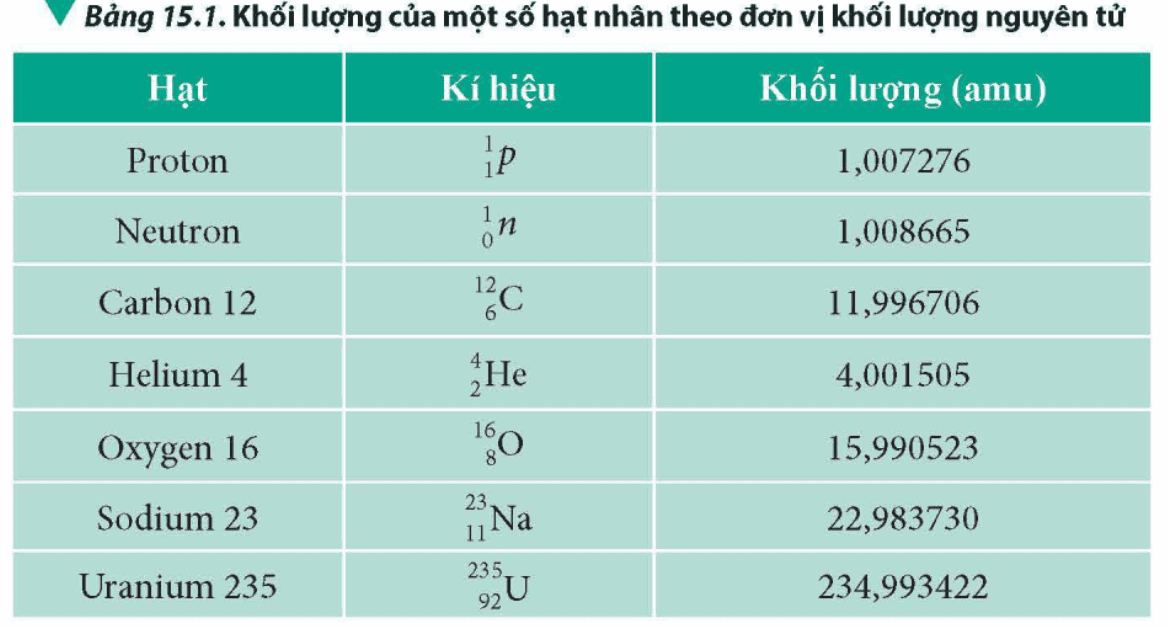
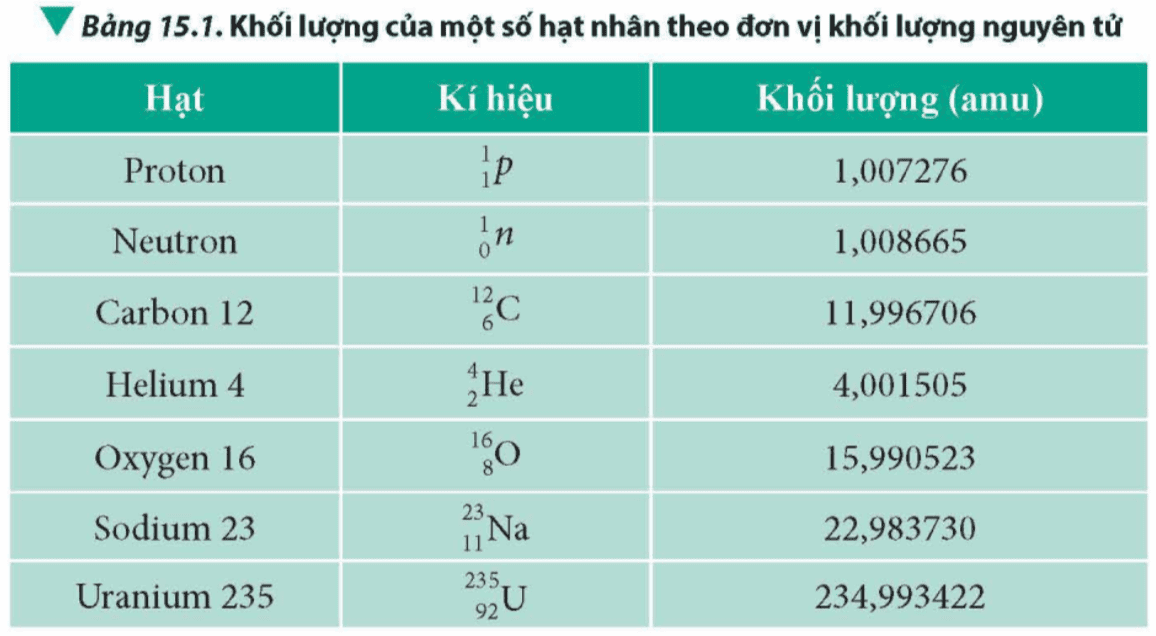
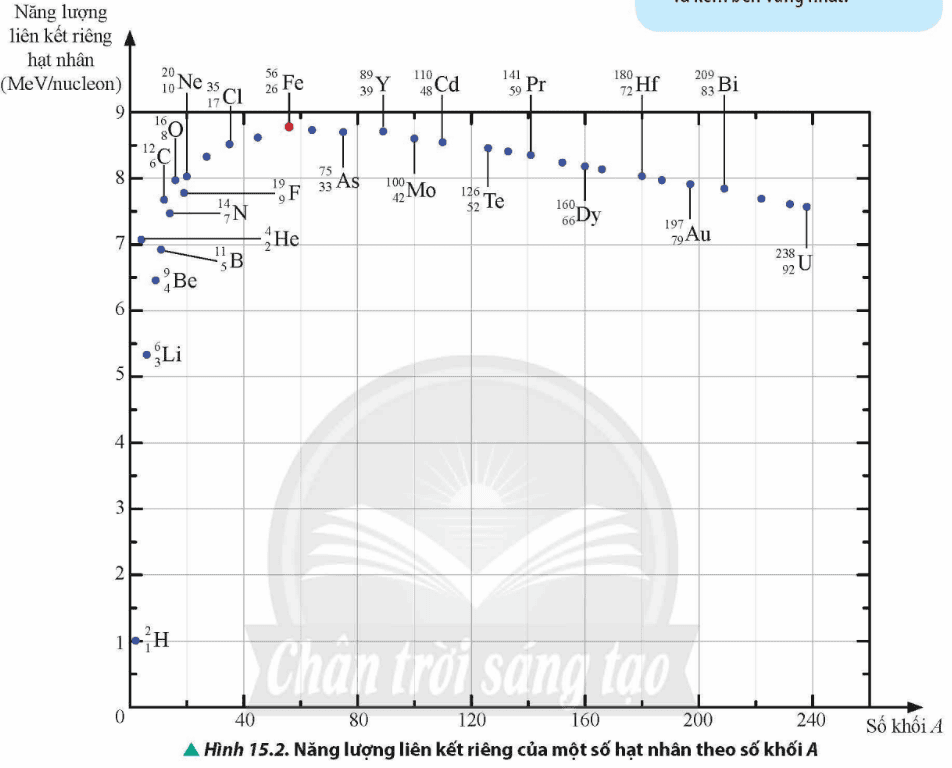
Ta đã biết hạt nhân gồm các proton mang điện dương và các neutron trung hoà về điện. Lực đẩy tĩnh điện giữa các proton là rất lớn vì khoảng cách giữa chúng rất nhỏ. Để duy trì sự tồn tại của hạt nhân, các proton và các neutron (các nucleon) cần một lực hút mạnh hơn lực đẩy tĩnh điện, lực này được gọi là lực hạt nhân. Vậy mức độ liên kết của các nucleon có giống nhau hay không đổi với các hạt nhân khác nhau? Độ bền vững của các hạt nhân được đánh giá dựa vào đại lượng vật lí nào?

Đáp án

Mức độ liên kết của các nucleon khác nhau đối với các hạt nhân khác nhau.

Độ bền vững của hạt nhân được đánh giá dựa trên năng lượng liên kết riêng của hạt nhân.

Thảo luận 1

100

Tính năng lượng nghỉ của một đồng xu có khối lượng 2 g đang nằm yên trên bàn theo hệ thức về mối liên hệ giữa khối lượng và năng lượng.

Đáp án

Năng lượng nghỉ của đồng xu: \(E_{0}=m_{0} c^{2}=2.10^{-3} \cdot\left(3.10^{8}\right)^{2}=1,8.10^{14} \mathrm{~J}\)

Luyện tập 1

101

Mặt Trời là một nguồn phát năng lượng khổng lồ với công suất rất lớn. Công suất trung bình của Mặt Trời khoảng \(4.10^{26}\) W. Hãy ước tính khối lượng Mặt Trời mất đi trong mỗi giây để tạo ra được công suất nói trên

Đáp án

Năng lượng của Mặt Trời trong 1 giây là: \(E=4.10^{26}(\mathrm{~J})\) Khối lượng Mặt Trời mất đi trong mỗi giây là:

\[m=\frac{E}{c^{2}}=\frac{4.10^{26}}{\left(3.10^{8}\right)^{2}}=4,44.10^{9} \mathrm{~kg}\]

Thảo luận 2

101

Hãy ước lượng khối lượng riêng của hạt nhân \({ }_{6}^{12} \mathrm{C}\). Nhận xét.

Đáp án

Thể tích hạt nhân: \(V=\frac{4}{3} \pi r^{3}=\frac{4}{3} \pi\left(1,2.10^{-15} \cdot 12^{\frac{1}{3}}\right)^{3}=8,69.10^{-44} \mathrm{~m}^{3}\)

Khối lượng hạt nhân: \(m=12 a m u=12.1,66.10^{-27}=1,99.10^{-26} \mathrm{~kg}\)

Khối lượng riêng hạt nhân: \(D=\frac{m}{V}=\frac{1,99.10^{-26}}{8,69.10^{-44}}=2,3.10^{17} \mathrm{~kg} / \mathrm{m}^{3}\)

Thảo luận 3

102

Sử dụng hệ thức \(E=m c^{2}\) để xác định năng lượng của các hạt trong Bảng 15.1 theo đơn vị MeV và J .

Đáp án

Hạt	Kí hiệu	Khối lượng (amu)	Năng lượng ( MeV)	Năng lượng (J)
Proton	\({ }_{1}^{1} \mathrm{H}\)	1,007276	938,28	\(1,51.10^{-10}\)
Neutron	\({ }_{0}^{1} n\)	1,008665	939,57	\(1,51.10^{-10}\)
Carbon 12	\({ }_{6}^{12} \mathrm{C}\)	11,996706	11174,93	\(1,79.10^{-9}\)
Helium 4	\({ }_{2}^{4} \mathrm{He}\)	4,001505	3727,4	\(5,98.10^{-10}\)
Oxygen 16	\({ }_{8}^{16} \mathrm{O}\)	15,990523	14895,17	\(2,39.10^{-9}\)
Sodium 23	\({ }_{11}^{23} \mathrm{Na}\)	22,983730	21409,34	\(2,68.10^{-8}\)
Uranium 235	\({ }_{92}^{235} \mathrm{U}\)	234,99342	218896,37	\(3,51.10^{-8}\)

Thảo luận 4

102

So sánh lực đẩy tĩnh điện và lực hấp dẫn giữa hai proton đặt cách nhau 1 fm. Biết rằng điện tích của proton là \(1,6.10^{-19}\) C và lực hấp dẫn giữa hai proton ở khoảng cách 1 fm là \(1,87 \cdot 10^{-34} \mathrm{~N}\).

Đáp án

Đổi: \(1 \mathrm{fm}=10^{-15} \mathrm{~m}\)

Lực đẩy tĩnh điện: \(F=k \frac{\left|q_{1} q_{2}\right|}{r^{2}}=9.10^{9} \cdot \frac{\left(1,6.10^{-19}\right)^{2}}{\left(10^{-15}\right)^{2}}=230,4 \mathrm{~N}\)

Lực hấp dẫn: \(F_{h d}=1,87 \cdot 10^{-34} \mathrm{~N}\)

Thảo luận 5

103

Tính độ hụt khối của hai hạt nhân bất kì được cho trong Bảng 15.1.

Đáp án

Đổi khối lượng: \(m_{p}=1,673.10^{-27} \mathrm{~kg}=1,00728 \mathrm{amu}\) \(m_{n}=1,675.10^{-27} \mathrm{~kg}=1,00866 \mathrm{amu}\)

Độ hụt khối của hạt nhân Carbon 12:

\[\Delta m=6.1,00728+6.1,00866-11,996706=0,099 a m u\]

Độ hụt khối của hạt nhân Helium 4:

\[\Delta m=2.1,00728+2.1,00866-4,001505=0,03 a m u\]

Thảo luận 6

103

Tính năng lượng liên kết của hai hạt nhân bất kì được cho trong Bảng 15.1

Đáp án

Năng lượng liên kết của hạt nhân Carbon 12:

\[E_{l k}=\Delta m c^{2}=0,099.931,5=92,22 \mathrm{MeV}\]

Năng lượng liên kết của hạt nhân Helium 4:

\[E_{l k}=\Delta m c^{2}=0,03.931,5=27,95 \mathrm{MeV}\]

Thảo luận 7

104

Tính năng lượng liên kết riêng của các hạt nhân \({ }_{6}^{12} C,{ }_{2}^{4} H e,{ }_{8}^{16} O,{ }_{92}^{235} U\) trong Bảng 15.1 và chỉ ra trong đó hạt nhân nào bển vững nhất và kém bền vững nhất.

Đáp án

\[\begin{array}{l}E_{l k r}=\frac{E_{l k}}{A}=\frac{\Delta m c^{2}}{A} \\E_{l k r(C)}=\frac{((6.1,007276+6.1,008665)-11,996706) .931,5}{12}=7,68 \mathrm{MeV} / \text { nucleon } \\E_{l k r(H e)}=\frac{((2.1,007276+2.1,008665)-4,001505) .931,5}{4}=7,07 \mathrm{MeV} / \text { nucleon } \\E_{l k r(O)}=\frac{((8.1,007276+8.1,008665)-15,990523) .931,5}{16}=7,98 \mathrm{MeV} / \text { nucleon } \\E_{l k r(U)}=\frac{((92.1,007276+143.1,008665)-234,993422) .931,5}{235}=7,59 \mathrm{MeV} / \text { nucleon }\end{array}\]

Hạt nhân bền vững nhất là \({ }_{8}^{16} \mathrm{O}\); Hạt nhân kém bền vững nhất là \({ }_{2}^{4} \mathrm{He}\)

Luyện tập 2

104

Hãy thảo luận và giải thích tại sao hạt nhân \({ }_{1}^{1} \mathrm{H}\) không xuất hiện trong Hình 15.2.

Đáp án

Vi hạt nhân \({ }_{1}^{1} H\) chỉ có 1 proton, 0 neutron nên không có năng lượng liên kết.

Vận dụng

104

a) Dựa vào Bảng 15.1, tính năng lượng liên kết và năng lượng liên kết riêng của hạt nhân \({ }_{26}^{56} \mathrm{Fe}\). Biết khối lượng của hạt nhân này là 55,934936 amu.

b) Từ kết quả câu a và Thảo luận 7, hãy so sánh mức độ bền vững của hạt nhân \({ }_{26}^{56} \mathrm{Fe}\) với các hạt nhân \({ }_{6}^{12} \mathrm{C},{ }_{2}^{4} \mathrm{He},{ }_{8}^{16} \mathrm{O}\) và \({ }_{92}^{235} \mathrm{U}\).

c) Kiểm tra kết quả câu b dựa vào Hình 15.2.

Đáp án

a) Độ hụt khối của hạt nhân \({ }_{26}^{56} \mathrm{Fe}\) là:

\[\Delta m=26 \cdot 1,00728+(56-26) \cdot 1,00866-55,934936=0,514 a m u\]

Năng lượng liên kết: \(E_{l k}=\Delta m c^{2}=0,514.931,5=478,791 \mathrm{MeV}\)Năng lượng liên kết riêng: \(E_{l k r}=\frac{E_{l k}}{A}=\frac{478,791}{56}=8,55 \mathrm{MeV} /\) nucleon

b) Hạt nhân \({ }_{26}^{56} \mathrm{Fe}\) bền vững hơn so với các hạt nhân \({ }_{6}^{12} \mathrm{C},{ }_{2}^{4} \mathrm{He},{ }_{8}^{16} \mathrm{O}\) và \({ }_{92}^{235} \mathrm{U}\).

c) Dựa vào hình vẽ xác định được năng lượng liên kết riêng của hạt nhân \({ }_{26}^{56} \mathrm{Fe}\) cỡ \(8,6 \mathrm{MeV} /\) nucleon, gần đúng so với tính toán.

Bài tập 1

104

Độ bền vững của hạt nhân phụ thuộc vào đại lượng vật lí nào?

A. Năng lượng liên kết.

B. Năng lượng liên kết riêng.

C. Độ hụt khối.

D. Số khối và số neutron.

Đáp án

Đáp án đúng là B

Độ bền vững của hạt nhân phụ thuộc vào năng lượng liên kết riêng.

Bài tập 2

104

Dựa vào Bảng 15.1, tính độ hụt khối, năng lượng liên kết và năng lượng liên kết riêng của hạt nhân \({ }_{82}^{206} \mathrm{~Pb}\). Biết khối lượng của hạt nhân này là 205,974466 amu.

Đáp án

Độ hụt khối:

\(\Delta m=82 \cdot 1,00728+(206-82) \cdot 1,00866-205,974466=1,696 a m u\)Năng lượng liên kết:

\(E_{l k}=\Delta m c^{2}=1,696.931,5=1574,235 \mathrm{MeV}\)Năng lượng liên kết riêng:

\(E_{l k r}=\frac{E_{i k}}{A}=\frac{1574,235}{206}=7,64 \mathrm{MeV} /\) nucleon