Mở đầu
22
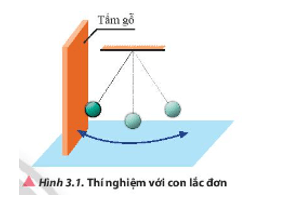
Tiến hành thí nghiệm như mô tả trong Hình 3.1. Đặt một tấm gỗ cố định lên tường, đưa vật nặng của con lắc đơn đến vị trí tiếp xúc với tấm gỗ và thả nhẹ để vật nặng bắt đầu chuyển động không vận tốc ban đầu. Khi dao động, vật nặng có va chạm vào tấm gỗ hay không? Vì sao? Trong quá trình dao động, vật nặng có những dạng năng lượng gì và sự chuyển hoá giữa chúng như thế nào?
Đáp án
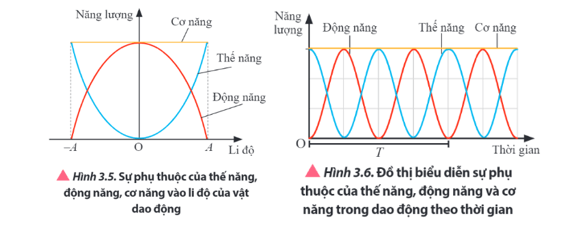
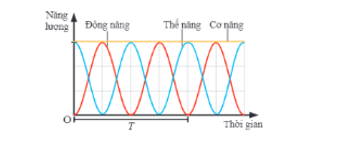
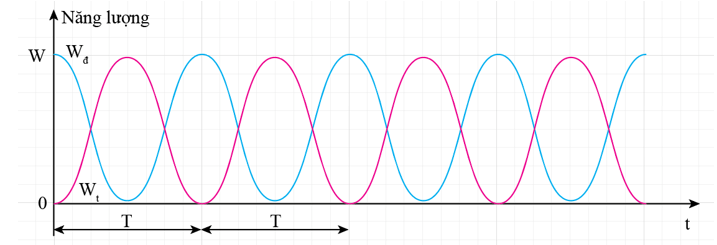
Nếu trong quá trình dao động, ta bỏ qua mọi ma sát thì vật nặng sẽ chạm vào tấm gỗ như lúc bắt đầu thả, khi đó coi như chỉ có sự chuyển hoá qua lại giữa động năng và thế năng.
Tuy nhiên về mặt thực tế thì không có trường hợp nào là hoàn toàn lí tưởng, nên sau mỗi chu kì dao động, năng lượng sẽ được chuyển hoá một phần thành năng lượng hao phí (nhiệt năng, năng lượng âm thanh) nên vật nặng không chạm vào tấm gỗ mà càng ngày càng có xu hướng trở về trạng thái cân bằng.