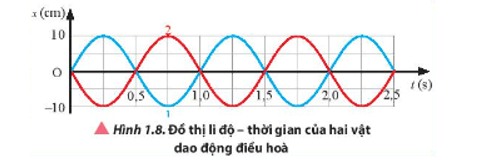
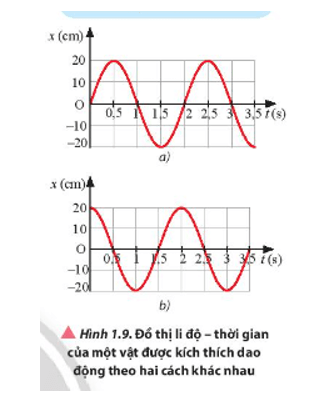
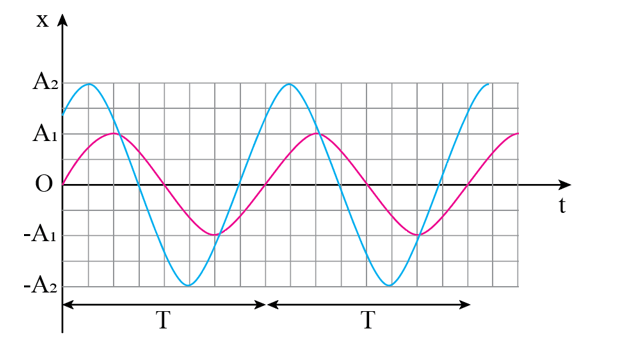
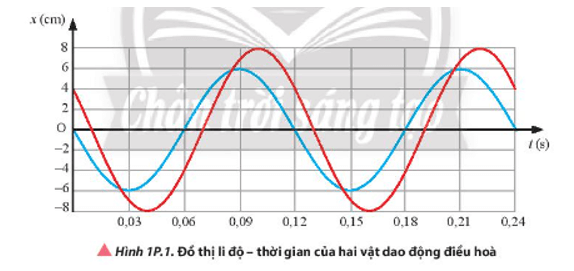
Mở đầu
5
Sự dao động của các vật diễn ra phổ biến trong cuộc sống hằng ngày như: dao động của quả lắc đồng hồ (Hình 1.1a), dao động của cánh chim ruồi để giữ cho cơ thể bay tại chỗ trong không trung khi hút mật (Hình 1.1b). Vậy dao động có đặc điểm gì và được mô tả như thế nào?

Đáp án
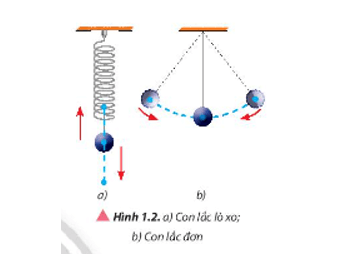
Dao động là sự chuyển động có giới hạn trong không gian của một vật quanh một vị trí xác định. Vị trí đó gọi là vị trí cân bằng.
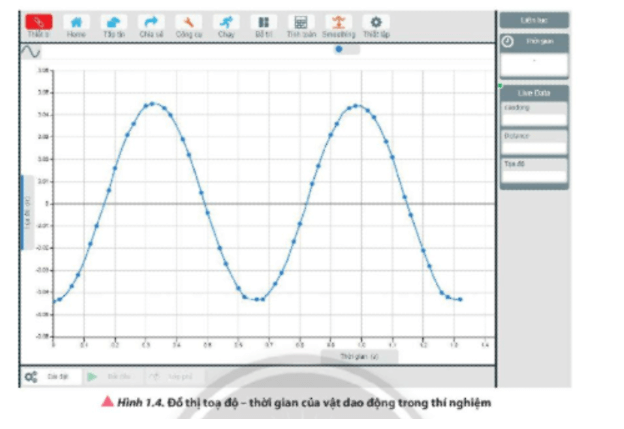
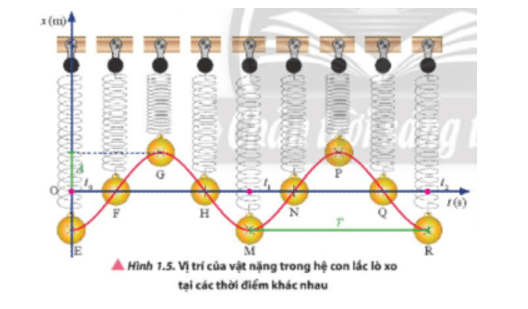
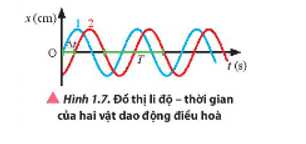
Dao động đó có thể được mô tả bằng lời hoặc thông qua các phương trình toán học dựa vào các thông tin như biên độ, li độ, tần số, chu kì.