88
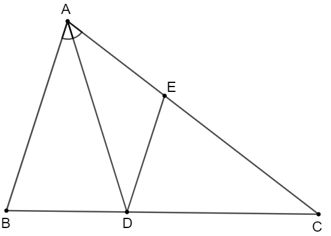
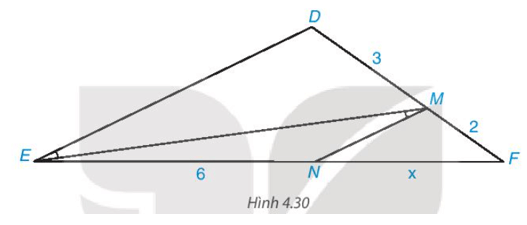
Tìm độ dài x trong Hình 4.30
Trong Hình 4.30 có \(\widehat{D E M}=\widehat{E M N}\) mà hai góc này ở vị trí so le trong nên \(\mathrm{MN}\) // DE.
Áp dụng định lí Thalès vào tam giác \(\mathrm{DEF}\) có \(\mathrm{MN} / / \mathrm{DE}\), ta có:
\(\frac{M F}{M D}=\frac{N F}{N E} \text { hay } \frac{2}{3}=\frac{x}{6} \text {. }\)
Suy ra \(x=\frac{2 \cdot 6}{3}=4\) (đvđd).
Vậy \(x=4\) (đvđd).
88
Cho tứ giác \(A B C D\), gọi \(E, F, K\) lần lượt là trung điểm của \(A D, B C, A C\).
a) Chứng minh \(\mathrm{EK} / / \mathrm{CD}, \mathrm{FK} / / \mathrm{AB}\).
b) So sánh EF và \(\frac{1}{2}(A B+C D)\).
a) Vì E, K lần lượt là trung điểm của AD, AC nên EK là đường trung bình của tam giác ACD suy ra EK // CD.
Vì K, F lần lượt là trung điểm của AC, BC nên KF là đường trung bình của tam giác ABC suy ra KF // AB.
Vậy EK // CD, FK // AB.
b) Vì EK là đường trung bình của tam giác ACD nên \(E K=\frac{1}{2} C D\);
Vì KF là đường trung bình của tam giác \(\mathrm{ABC}\) nên \(K F=\frac{1}{2} A B\).
Do đó \(E K+K F=\frac{1}{2}(A B+C D)\)
Áp dụng bất đẳng thức tam giác vào tam giác KEF, ta có: \(E F<E K+K F\)
Từ (1) và (2) ta suy ra \(E F<\frac{1}{2}(A B+C D)\).
88
Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng \(\frac{AC}{AB}=\frac{EC}{EA}\)
Theo đề bài, \(A D\) là tia phân giác của \(\widehat{B A C}\), áp dụng tính chất đường phân giác vào tam giác \(\mathrm{ABC}\), ta có: \(\frac{A C}{A B}=\frac{D C}{D B}\)
Đường thẳng qua \(\mathrm{D}\) song song với \(\mathrm{AB}\) cắt \(\mathrm{AC}\) tại \(\mathrm{E}\) hay \(\mathrm{DE} / / \mathrm{AB}\), áp dụng định lí Thalès vào tam giác \(A B C\), ta có: \(\frac{D C}{D B}=\frac{E C}{E A}\)
Từ (1) và (2) suy ra \(\frac{A C}{A B}=\frac{E C}{E A}\) (đpcm).
88
Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt BC tại D.
a) Tính độ dài đoạn thẳng DB và DC.
b) Tính tỉ số diện tích của hai tam giác ABD và ACD.
a) Áp dụng tính chất đường phân giác, ta có:
\(\frac{D B}{D C}=\frac{A B}{A C}=\frac{15}{20}=\frac{3}{4}\)
Suy ra \(\frac{D B}{3}=\frac{D C}{4}\).
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{D B}{3}=\frac{D C}{4}=\frac{D B+D C}{3+4}=\frac{B C}{7}=\frac{25}{7} \text {. }\)
Do đó, \(D B=\frac{25.3}{7}=\frac{75}{7}(\mathrm{~cm}) ; D C=\frac{25.4}{7}=\frac{100}{7}(\mathrm{~cm})\).
Vậy \(D B=\frac{75}{7} \mathrm{~cm} ; D C=\frac{100}{7} \mathrm{~cm}\).
b) Hai tam giác \(A B D\) và \(A C D\) có chung đường cao kẻ từ đỉnh \(A\) đến cạnh \(B C\), ta gọi đường cao đó là \(\mathrm{AH}\).
Ta có: \(S_{A B D}=\frac{1}{2} A H . D B ; S_{A D C}=\frac{1}{2} A H . D C\).
Suy ra \(\frac{S_{A B D}}{S_{A D C}}=\frac{\frac{1}{2} A H \cdot B D}{\frac{1}{2} A H \cdot D C}=\frac{D B}{D C}=\frac{3}{4}\).
Vậy tỉ số diện tích của hai tam giác ABD và ACD bằng \(\frac{3}{4}\).
88
Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: \(DM^2=MN.MK\)
Vì \(A B C D\) là hình bình hành nên \(A B / / C D, A D / / B C\) suy ra \(A N / / c D, a d / / c k\).
Áp dụng định lí Thalès vào tam giác \(A M N\) có \(\mathrm{AN} / / \mathrm{CD}\), ta được:
\(\frac{D M}{M N}=\frac{C M}{A M}\)
Áp dụng định lí Thalès vào tam giác \(A D M\) có \(C K / / A D\), ta được:
\(\frac{M K}{D M}=\frac{C M}{A M}\)
Từ (1) và (2) suy ra: \(\frac{D M}{M N}=\frac{M K}{D M}=\frac{C M}{A M}\).
Do đó \(\mathrm{DM}^2=\mathrm{MN} \cdot \mathrm{MK}(đpcm)\)
