Bài 3.19
63
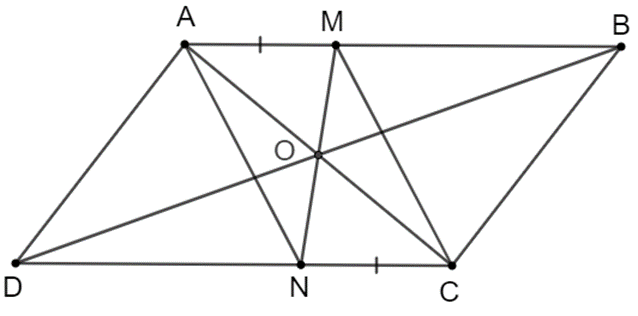
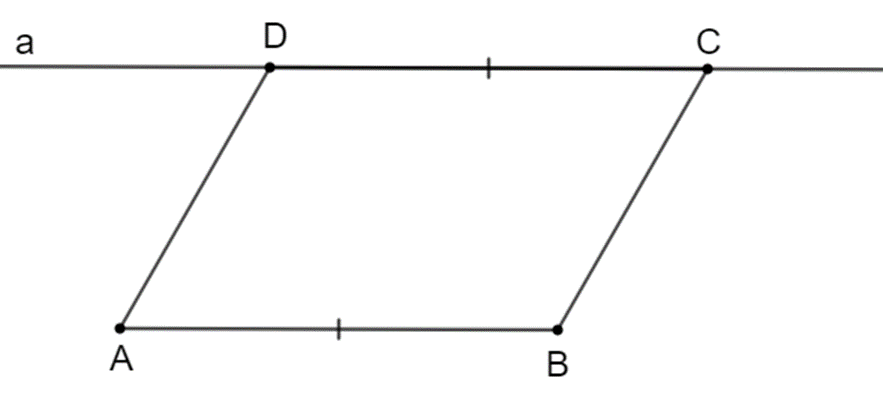
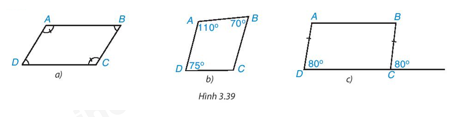
Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?
Gợi ý
Sử dụng tính chất của hình bình hành
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
và định lí tổng các góc trong một tứ giác bằng \(360^{\circ}\)
Đáp án
* Hình 3.36 a)
Tứ giác \(\mathrm{ABCD}\) có: \(\widehat{A}=\widehat{C}=100^{\circ} ; \widehat{B}=\widehat{D}=80^{\circ}\)
Do đó, tứ giác \(A B C D\) là hình bình hành.
* Hình 3.36 b)
Tứ giác \(\mathrm{ABCD}\) có: \(\widehat{B} \neq \widehat{D}\left(70^{\circ} \neq 75^{\circ}\right)\).
Do đó, tứ giác \(A B C D\) không là hình bình hành.
* Hình 3.36 c)
Đặt \(\widehat{B C \mathrm{x}}=80^{\circ}\) (như hình vẽ)
Ta có: \(\widehat{D}=\widehat{B C \mathrm{x}}=80^{\circ}\) mà hai góc này ở vị trí đồng vị nên \(\mathrm{AD} / /\) BC.
Tứ giác \(\mathrm{ABCD}\) có:
- \(A D / / B C\) (chứng minh trên)
- \(A D=B C\) (giả thiết)
Do đó, tứ giác \(A B C D\) là hình bình hành.
Vậy tứ giác \(A B C D\) trong Hình 3.36 a) và 3.36 c) là hình bình hành; tứ giác \(A B C D\) trong Hình 3.36b) không là hình bình hành.