121
Tính thể tích của hình chóp tam giác đều S.ABC, biết diện tích đáy của nó bằng 15,6 cm2, chiều cao bằng 10 cm.
Thể tích của khối chóp tam giác đều S.ABC là
\(V=\frac{1}{3} S \cdot h=\frac{1}{3} \cdot 15,6 \cdot 10=52\left(\mathrm{~cm}^3\right) .\)
122
Trong các miếng bìa ở Hình 10.32, miếng bìa nào khi gấp và dán lại thì được một hình chóp tam giác đều, miếng nào thì được một hình chóp tứ giác đều.
Miếng bìa 4 gấp và dán lại được hình chóp tam giác đều.
Miếng bìa 2 gấp và dán lại được hình chóp tứ giác đều.
Miếng bìa 1 và miếng bìa 3 không không có đáy là hình vuông hay hình tam giác nên không thỏa mãn.
122
Tính thể tích hình chóp tam giác đều A.BCD có độ dài cạnh đáy bằng 10 cm, chiều cao bằng 12 cm (H.10.33), biết √75≈8,66
Vì l là trung điểm của \(B C\) nên \(B I=I C=10: 2=5 \mathrm{~cm}\).
Xét tam giác BID vuông tại I, có \(\left|D^2+B\right|^2=B D^2\) (định lí Pythagore).
Suy ra \(I D^2=B D^2-B I^2=10^2-5^2=75\).
Do đó, \(\mathrm{ID}=\sqrt{75} \approx 8,66(\mathrm{~cm})\).
Diện tích tam giác đáy BCD là:
\(S_{B C D}=\frac{1}{2} \cdot I D \cdot B C \approx \frac{1}{2} \cdot 8,66 \cdot 10=43,3\left(\mathrm{~cm}^2\right) \text {. }\)
Thể tích hình chóp tam giác đều A.BCD là:
\(\mathrm{V}=\frac{1}{3} \cdot \mathrm{S} \cdot \mathrm{h} \approx \frac{1}{3} \cdot 43,3 \cdot 12=173,2\left(\mathrm{~cm}^3\right)\)
122
Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.
a) Tính thể tích hình chóp.
b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết rằng người ta đo được độ dài cạnh bên của hình chóp là 31,92 m.
a) Thể tích hình chóp tứ giác đều là:
b) Mô tả hình chóp như hình dưới đây.
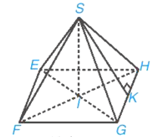
Ta có \(\mathrm{SI}=21 \mathrm{~m}, \mathrm{EF}=\mathrm{FG}=\mathrm{GH}=\mathrm{HE}=34 \mathrm{~m}, \mathrm{SE}=\mathrm{SF}=\mathrm{SG}=\mathrm{SH}=31,92 \mathrm{~m}\)
SK là một trung đoạn của hình chóp.
K là trung điếm của \(\mathrm{GH}\) nên \(\mathrm{GK}=\mathrm{KH}=\frac{G H}{2}=\frac{34}{2}=17 \mathrm{~m}\).
Áp dụng định lí Pythagore cho tam giác SKH vuông tại H, ta có:
\(\mathrm{KH}^2+5 \mathrm{~K}^2=\mathrm{SH}^2\)
Hay \(17^2+\mathrm{SK}^2=(31,92)^2\)
Suy ra \(\mathrm{SK}^2=(31,92)^2-17^2 \approx 729,89\). Do đó, \(\mathrm{SK} \approx 27,02 \mathrm{~m}\).
Diện tích xung quanh của hình chóp tứ giác đều hay tống diện tích các tấm kính đế phủ kín bốn mặt bên hình chóp này là:
\(S_{x q}=p \cdot d=\frac{34 \cdot 4}{2} \cdot 27,02=1837,36\left(\mathrm{~m}^2\right) .\)
