Câu hỏi 9.32
109
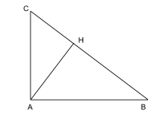
Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm.
a) Tính độ dài đoạn thẳng AH.
b) Tính độ dài các đoạn thẳng AB và AC.
Đáp án
a) Có \(\mathrm{BC}=\mathrm{BH}+\mathrm{CH}=16+9=25(\mathrm{~cm})\).
Xét tam giác \(A B C\) vuông tại \(A\) có: \(A B^2+A C^2=B C^2\) (định lý Pythagore).
Xét tam giác \(\mathrm{AHC}\) vuông tại \(\mathrm{H}\) có: \(\mathrm{AC}^2=\mathrm{AH}^2+\mathrm{CH}^2\) (định lý Pythagore).
Suy ra \(\mathrm{AH}^2=\mathrm{AC}^2-\mathrm{CH}^2\) (1).
Xét tam giác AHB vuông tại \(\mathrm{H}\) có: \(\mathrm{AH}^2+\mathrm{BH}^2=\mathrm{AB}^2\) (định lý Pythagore).
Suy ra \(\mathrm{AH}^2=\mathrm{AB}^2-\mathrm{BH}^2(2)\).
Xét (1) + (2), có:
\(\begin{aligned}& 2 \mathrm{AH}^2=\mathrm{AC}^2-\mathrm{CH}^2+\mathrm{AB}^2-\mathrm{BH}^2 \\& 2 \mathrm{AH}^2=\mathrm{BC}^2-\mathrm{CH}^2-\mathrm{BH}^2 \quad\left(\text { vil } \mathrm{AB}^2+\mathrm{AC}^2=\mathrm{BC}^2\right) \\& 2 \mathrm{AH}^2=25^2-9^2-16^2 \\& 2 \mathrm{AH}^2=288 \\& \mathrm{AH}^2=144\end{aligned}\)
Suy ra \(\mathrm{AH}=12(\mathrm{~cm})\).
b) Có \(\mathrm{AC}^2=\mathrm{AH}^2+\mathrm{CH}^2=12^2+9^2=225\).
Suy ra \(\mathrm{AC}=15(\mathrm{~cm})\).
\(\text { Có } A B^2=A H^2+B H^2=12^2+16^2=400 \text {. }\)
Suy ra \(A B=20(\mathrm{~cm})\).