Bài tập cuối chương IX

Vì ΔA′B′C′ ∽ ΔABC nên đỉnh A' tương ứng với đỉnh A, đỉnh B' tương ứng với đỉnh B, đỉnh C' tương ứng với đỉnh C. Vậy xét các đáp án ta thấy khẳng định A là khẳng định đúng do các cặp đỉnh tương ứng với nhau theo thứ tự trên.

Đáp án đúng là C
Vi \(\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} C^{\prime} \sim \triangle \mathrm{ABC}\), suy ra \(\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{B^{\prime} C^{\prime}}{B C}=2\).

Xét đáp án B ta thấy \(6^2 + 8^2 = 10^2\) (= 100) nên bộ ba này tạo thành tam giác vuông.

(theo định lí Pythagore đảo).

Đáp án đúng là C

Xét từng đáp án:

+ Hai tam giác \(\mathrm{ABC}\) vuông ở \(\mathrm{A}\) và \(\mathrm{DEF}\) vuông ở \(\mathrm{D}\) có \(\widehat{B}=\widehat{E}\) thì \(\triangle \mathrm{ABC} \sim \triangle \mathrm{DEF}\).
+ Hai tam giác \(\mathrm{ABC}\) vuông ở \(\mathrm{A}\) và \(\mathrm{DEF}\) vuông ở \(\mathrm{D}\) có \(\widehat{C}=\widehat{F}\) thì \(\triangle \mathrm{ABC} \backsim \triangle \mathrm{DEF}\).
Do đó, dữ kiện ở hai đáp án \(\mathrm{A}\) và \(\mathrm{B}\) suy ra \(\triangle \mathrm{ABC} \sim \triangle \mathrm{DEF}\).
+ Xét đáp án D: Vì tam giác \(\mathrm{ABC}\) vuông ở A nên \(\widehat{B}+\widehat{C}=90^{\circ}\);
Tam giác DEF vuông ở D nên \(\widehat{E}+\widehat{F}=90^{\circ}\).
Do đó, \(\widehat{B}+\widehat{C}=\widehat{E}+\widehat{F}\).
Mà ta có \(\widehat{B}-\widehat{C}=\widehat{E}-\widehat{F}\).
Cộng vế theo vế ta được \(2 \widehat{B}=2 \widehat{E}\) hay \(\widehat{B}=\widehat{E}\). Khi đó \(\triangle \mathrm{ABC} \sim \triangle \mathrm{DEF}\).
+ Dữ kiện ở đáp án C luôn xảy ra với mọi cặp tam giác vuông nên từ dữ kiện này không suy ra được \(\triangle \mathrm{ABC} \backsim \triangle \mathrm{DEF}\).

+) ΔCNM ∽ ΔCAB (vì MN // AB) (1).

+) ΔMPB ∽ ΔCAB (vì MP // AC) (2).

+) Từ (1) và (2) ta suy ra được ΔCNM ∽ ΔMPB.

- Xét tam giác \(A B D\) và tam giác \(A C E\) có \(\widehat{A B D}=\widehat{A C E}\) (giả thiết), góc A chung.

Suy ra \(\triangle A B D \sim \triangle A C E(g . g)\).
- vì \(\triangle A B D \sim \triangle A C E\) nên \(\widehat{A D B}=\widehat{A E C}\).

Suy ra \(\widehat{C D O}=\widehat{B E O}\) (1).
Lại có \(\widehat{B O E}=\widehat{C O D}\) (hai góc đới đỉnh) (2).
Từ (1) và (2) suy ra \(\triangle \mathrm{BOE} \backsim \triangle \mathrm{COD}\) (g.g).

Vì \(\mathrm{BM}, \mathrm{CN}\) là các đường trung tuyến của tam giác \(\mathrm{ABC}\) nên \(\mathrm{M}, \mathrm{N}\) lần lượt là trung điểm của \(A C, A B\).

Suy ra \(\mathrm{MN}\) là đường trung bình của tam giác \(\mathrm{ABC}\).
Do đó, \(\mathrm{MN} / / \mathrm{BC}\).
Suy ra \(\widehat{G M N}=\widehat{G B C}\) (hai góc ở vị trí so le trong).
Mặt khác \(\widehat{N G M}=\widehat{C G B}\) (hai góc đối đỉnh).
Do đó, \(\triangle \mathrm{GMN} \sim \Delta \mathrm{GBC}\) (g.g).
Vì \(\mathrm{MN}\) là đường trung bình của tam giác \(\mathrm{ABC}\) nên \(\mathrm{BC}=2 \mathrm{MN}\).
Khi đó, \(\frac{G N}{G C}=\frac{G M}{G B}=\frac{M N}{B C}=\frac{1}{2}\).
Vậy \(\triangle \mathrm{GMN} \sim \triangle \mathrm{GBC}\) với tỉ số đồng dạng bằng \(\frac{1}{2}\).

a) Ta có \(\widehat{D A H}+\widehat{H A C}=\widehat{B A C}=90^{\circ} \widehat{A C H}+\widehat{H A C}=90^{\circ}\) (do tam giác ACH vuông ở \(\mathrm{H}\) ). Suy ra \(\widehat{D A H}=\widehat{A C H}\) (cùng phụ với \(\widehat{H A C}\) ).

Tam giác HDA vuông tại \(\mathrm{D}\) và tam giác \(\mathrm{AHC}\) vuông tại \(\mathrm{H}\) có \(\widehat{D A H}=\widehat{A C H}\) nên \(\triangle \mathrm{HDA} \backsim \triangle \mathrm{AHC}\).
b) Áp dụng định lí Pythagore cho tam giác vuông \(A B C\), ta có
\(B C^2=A B^2+A C^2=4^2+5^2=41\).
Suy ra \(B C=\sqrt{41} \mathrm{~cm}\).
Diện tích tam giác \(A B C\) là: \(S_{A B C}=\frac{A B \cdot A C}{2}=\frac{4 \cdot 5}{2}=10\left(\mathrm{~cm}^2\right)\).
Lại có \(S_{A B C}=\frac{A H \cdot B C}{2}\), do đó \(\mathrm{AH} \cdot \mathrm{BC}=2 \cdot 10=20\), suy ra \(\mathrm{AH}=\frac{20}{B C}=\frac{20}{\sqrt{41}}(\mathrm{~cm})\).
Áp dụng định lí Pythagore cho tam giác \(\mathrm{ACH}\) ta có \(\mathrm{AC}^2=\mathrm{AH}^2+\mathrm{CH}^2\).
Do đó, \(\mathrm{CH}^2=\mathrm{AC}^2-\mathrm{AH}^2=4^2-\left(\frac{20}{\sqrt{41}}\right)^2=\frac{256}{41}\).
Suy ra \(C H=\frac{16}{\sqrt{41}}(\mathrm{~cm})\).
Vì \(\triangle \mathrm{HDA} \sim \triangle \mathrm{AHC}\) nên \(\frac{H D}{A H}=\frac{H A}{A C} \Rightarrow H D=\frac{A H^2}{A C}=\frac{\frac{400}{41}}{4}=\frac{100}{41}(\mathrm{~cm})\).
Ta có \(\mathrm{BH}=\mathrm{BC}-\mathrm{HC}=\sqrt{41}-\frac{16}{\sqrt{41}}=\frac{25}{\sqrt{41}}(\mathrm{~cm})\).

a) Xét tam giác AHB vuông tại H, có:

\(\mathrm{AH}^2+\mathrm{HB}^2=\mathrm{AB}^2\) (định lý Pythagore)
Suy ra \(A B^2=12^2+16^2=400\).
Suy ra \(\mathrm{AB}=20 \mathrm{~cm}\).
Tương tự, có: \(\mathrm{AC}^2=\mathrm{AH}^2+\mathrm{CH}^2\) (áp dụng định lý Pythagore trong tam giác vuông \(\mathrm{AHC}\) ).
Suy ra \(A C^2=12^2+9^2=225\).
Suy ra \(\mathrm{AC}=15 \mathrm{~cm}\).
Có \(\mathrm{BC}=\mathrm{CH}+\mathrm{BH}=9+16=25 \mathrm{~cm}\).
Trong tam giác \(\mathrm{ABC}\), nhận thấy \(\mathrm{AB}^2+\mathrm{AC}^2=\mathrm{BC}^2\) (do \(\left.20^2+15^2=25^2=625\right)\).
Suy ra tam giác ABC vuông tại A (định lí Pythagore đảo).
b) Xét tam giác AHB có:
\(\mathrm{M}\) là trung điếm của \(\mathrm{AH}\)
\(\mathrm{N}\) là trung điếm của \(\mathrm{BH}\)
Suy ra MN là đường trung bình của tam giác AHB.
Do đó, \(M N / / A B\). Mà \(A B \perp A C\) (vì tam giác \(A B C\) vuông tại \(A\) ).
Suy ra \(\mathrm{MN} \perp \mathrm{AC}\).
Xét \(\triangle A C N\) có \(A H \perp C N(g t), M N \perp A C(c m t), A H \cap M N=\{M\}\).
Vậy \(\mathrm{M}\) là trực tâm của \(\triangle \mathrm{ACN}\), do đó \(\mathrm{CM} \perp \mathrm{AN}\)
c) Ta có \(S_{\mathrm{AMN}}=\frac{A M \cdot H N}{2}=\frac{\frac{A H}{2} \cdot \frac{B H}{2}}{2}=\frac{A H \cdot B H}{8}=\frac{12 \cdot 16}{8}=24\left(\mathrm{~cm}^2\right)\).

a) Vì AD là tia phân giác của góc \(B A C\) nên \(\frac{B D}{D C}=\frac{A B}{A C}\).

Suy ra BD \(\cdot A C=D C \cdot A B \cdot\left({ }^*\right)\)
\(\begin{aligned}&  B D \cdot(A B+A C)=B D \cdot A B+B D \cdot A C \\& =B D \cdot A B+D C \cdot A B \quad\left(d o\left(^*\right)\right) \\& =A B \cdot(B D+D C) \\& =A B \cdot B C .\end{aligned}\)

Vậy \(\mathrm{BD} \cdot(\mathrm{AB}+\mathrm{AC})=\mathrm{AB} \cdot \mathrm{BC}\). Suy ra \(\frac{B D}{B C}=\frac{A B}{A B+A C}\).
Hai tam giác CED vuông tại E và tam giác CAB vuông tại A có góc nhọn C chung nên \(\Delta \mathrm{CED} \sim \Delta \mathrm{CAB}\).

Suy ra \(\frac{C E}{C A}=\frac{C D}{C B} \Rightarrow \frac{A C-A E}{A C}=\frac{B C-B D}{B C} \Rightarrow 1-\frac{A E}{A C}=1-\frac{D B}{B C}\).
Do đó, \(\frac{A E}{A C}=\frac{D B}{B C}\). (2)
Từ (1) và (2) suy ra \(\frac{A E}{A C}=\frac{A B}{A B+A C}\), do đó \(A E=\frac{A B \cdot A C}{A B+A C}\).
b) Hai tam giác DFC vuông tại D và tam giác ABC vuông tại \(A\) có góc nhọn \(C\) chung nên \(\triangle \mathrm{DFC} \sim \triangle \mathrm{ABC}\).
c) Vì \(\triangle \mathrm{DFC} \backsim \triangle \mathrm{ABC}\) nên \(\frac{D F}{A B}=\frac{D C}{A C} \Rightarrow D F=\frac{A B \cdot D C}{A C}\).

Từ \(\left({ }^*\right)\) ta có \(D B=\frac{D C \cdot A B}{A C}\).
Từ (3) và (4) suy ra DB = DF.

Giả sử AB là chiều cao của kim tự tháp với BC là bóng; A'B' là chiều cao cây cọc với bóng của nó trên mặt đất là B'C'.

Vì trong cùng một thời điểm, các tia nắng mặt trời tạo với mặt đất các góc bằng nhau.

Suy ra \(\widehat{B A C}=\widehat{B^{\prime} A^{\prime} C^{\prime}}\).
Xét hai tam giác \(B A C\) (vuông tại \(B\) ) và tam giác \(B^{\prime} A^{\prime} C^{\prime}\) (vuông tại \(B^{\prime}\) ) có \(\widehat{B A C}=\widehat{B^{\prime} A^{\prime} C}\), Suy ra \(\triangle B^{\prime} A^{\prime} C^{\prime} \sim \triangle B A C\).

Do đó, \(\frac{A^{\prime} B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C} \Rightarrow \frac{1}{A B}=\frac{1,5}{208,2}\)
Suy ra \(A B=208,2: 1,5=138,8(m)\).
Vậy kim tự tháp cao 138,8 m.

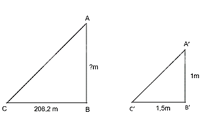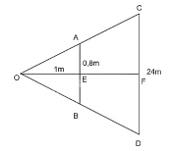
Giả sử O là vị trí bạn Lan đứng, AB là độ cao cửa sổ của nhà Lan, CD là độ cao của 6 tầng nhà đối diện mà Lan nhìn thấy. OE là khoảng cách từ vị trí bạn Lan đứng đến cửa sổ. OE cắt CD tại F.

Các điểm kí hiệu như trên hình vẽ.

Có OE = 1 m; AB = 80 cm = 0,8 m; CD = 6 ∙ 4 = 24 m.

Xét tam giác OAB và tam giác OCD có AB // CD (do các tòa nhà thẳng đứng vuông góc với mặt đất). Suy ra ΔOAB ∽ ΔOCD.

Do đó, \(\frac{O A}{O C}=\frac{A B}{C D}\).
Xét tam giác \(\mathrm{OAE}\) và tam giác OCF có \(\mathrm{AE} / / \mathrm{CF}\) (do \(\mathrm{AB} / / \mathrm{CD}\) ). Suy ra \(\triangle \mathrm{OAE} \sim \triangle \mathrm{OCF}\).
Do đó, \(\frac{O E}{O F}=\frac{O A}{O C}=\frac{A B}{C D} \Rightarrow \frac{1}{O F}=\frac{0,8}{24}\).
Suy ra \(O F=24: 0,8=30(\mathrm{~m})\).
Do đó, \(E F=O F-O E=30-1=29(m)\).
Vậy khoảng cách từ căn hộ nhà Lan đến tòa nhà đối diện là 29 m.