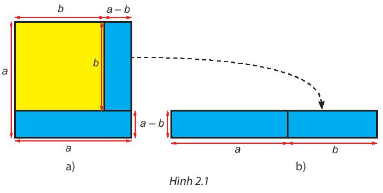
Luyện tập 1
30
Trong các đẳng thức sau, đẳng thức nào là hằng đẳng thức?
a) \(a(a+2 b)=a^2+2 a b\)
b) \(a+1=3 a-1\)
Gợi ý
Hằng đẳng thức là đẳng thức mà hai vế luôn cùng nhận một giá trị khi thay các chữ trong đẳng thức bằng các số tùy ý.
Đáp án
a) \(a(a+2 b)=a^2+2 a b\) là hằng đẳng thức.
b) \(a+1=3 a-1\) không là hằng đẳng thức vì khi ta thay \(a=2\) thì hai vế của đẳng thức không bằng nhau.