Hoạt động 1
104
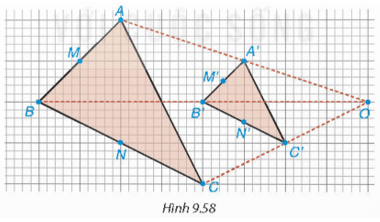
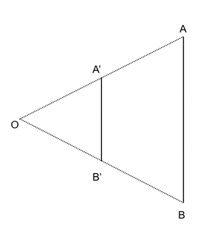
Lấy điểm O và vẽ tam giác A'B'C' như Hình 9.58. Trên các tia OA', OB', OC', lấy các điểm A, B, C sao cho OA = 2OA', OB = 2OB', OC = 2OC'.
- Hãy giải thích vì sao ΔABC ∽ ΔA'B'C' với tỉ số đồng dạng bằng 2.
- Dùng thước thẳng, em hãy kiểm tra xem đường thẳng MM', NN' nối các trung điểm có đi qua O không?
Đáp án
Dùng thước thẳng nối hai điểm tương ứng tùy ý trên hai hình, chẳng hạn C và C', ta thấy đường thẳng đi qua hai điểm này có đi qua \(\mathrm{O}\).
- Theo giả thiết ta suy ra được A' là trung điểm của \(O A, B^{\prime}\) là trung điểm \(O B\) và C' là trung điểm \(O C\) nên theo tính chất đường trung bình trong các tam giác \(O A B, O B C\) và \(\mathrm{OAC}\), suy \(\mathrm{ra} \frac{A B}{A^{\prime} B^{\prime}}=\frac{B C}{B^{\prime} C^{\prime}}=\frac{A C}{A^{\prime} C^{\prime}}=2\)
Suy ra \(\triangle \mathrm{ABC} \sim \triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime}\) (c.c.c) với tỉ số đồng dạng bằng 2.
- Các đường thẳng MM', NN' có đi qua O.