Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Qua bài này, các em sẽ có câu trả lời cho câu hỏi trên.

Tham khảo ở Luyện tập 1 trang 99.

+ Hai tam giác \(A B C\) (vuông tại \(A\) ) và tam giác XZY (vuông tại \(X\) ) có: \(\widehat{B}=\widehat{Z}=60^{\circ}\) Do đó \(\triangle \mathrm{ABC} \backsim \triangle \mathrm{XZY}\).
+ Hai tam giác DEF (vuông tại D) và tam giác GKH (vuông tại G) có: \(\frac{D E}{G K}=\frac{D F}{G H}=\frac{1}{2}\) Do đó \(\triangle \mathrm{DEF} \sim \Delta \mathrm{GKH}\).

a) Hai tam giác \(A B C\) vuông tại \(A\) và tam giác \(A^{\prime} B^{\prime} C^{\prime}\) vuông tại \(A^{\prime}\) có \(\widehat{B}=\widehat{B^{\prime}}\) (giả thiết) nên \(\triangle A B C \sim \triangle A^{\prime} B^{\prime} C^{\prime}\).
b) Ta có \(70 \mathrm{~cm}=0,7 \mathrm{~m}\).

Vì \(\triangle \mathrm{ABC} \sim \Delta \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime}\) nên \(\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C} \Rightarrow \frac{0,7}{6}=\frac{1,4}{A C}\).
Suy ra \(A C=6 \cdot 1,4: 0,7=12(\mathrm{~m})\).

Ta có \(C X=2,4-1,6=0,8(m)\).
\(M Y=1+19=20(\mathrm{~m}) \text {. }\)

Xét tam giác MXC và tam giác MYA có:
\(\widehat{M}\) chung
\(\widehat{M X C}=\widehat{M Y A}\)

Do đó: \(\triangle \mathrm{MXC} \sim \Delta \mathrm{MYA}(\mathrm{g} . \mathrm{g})\).
Suy ra \(\frac{C X}{A Y}=\frac{M X}{M Y}\). Do đó, \(A Y=\frac{C X \cdot M Y}{M X}=\frac{0,8 \cdot 20}{1}=16(\mathrm{~m})\).
Vậy chiều cao của cây là \(A B=A Y+Y B=A Y+M D=16+1,6=17,6 m\).

- Ta có: \(\frac{A^{\prime} B^{\prime}}{A B}=\frac{B^{\prime} H^{\prime}}{B H}=\frac{1}{2}\).
- Áp dụng định lí Pythagore cho tam giác vuông \(\mathrm{ABH}\) ta có: \(\mathrm{AH}^2+\mathrm{BH}^2=\mathrm{AB} \mathrm{B}^2\), suy ra \(A H^2=A B^2-B H^2=13^2-5^2=144\).

Suy ra \(\mathrm{AH}=12(\mathrm{~m})\).
- Tương tự ta có: \(A^{\prime} H^{\prime 2}=A^{\prime} B^{\prime 2}-B^{\prime} H^{\prime 2}=(6,5)^2-(2,5)^2=36\). Suy ra \(A^{\prime} H^{\prime}=6(m)\).
- Vậy \(\frac{A^{\prime} H^{\prime}}{A H}=\frac{1}{2}=\frac{B^{\prime} H^{\prime}}{B H}\).

Do đó hai tam giác vuông \(A^{\prime} H^{\prime} B^{\prime}\) và \(A H B\) đồng dạng, suy ra \(\widehat{A}=\widehat{A^{\prime}}\).
Vậy hai con dốc có độ dốc như nhau.

Ta có: \(\triangle \mathrm{ACB} \sim \triangle \mathrm{DEF}\) vì \(\frac{A C}{D E}=\frac{B C}{F E}=\frac{3}{2}\).
Hai tam giác MNP và DEF không đồng dạng với nhau vì ta tính được NP \(=\sqrt{29,25}\) nên \(\frac{M N}{D E} \neq \frac{N P}{F E}\), tương tự hai tam giác \(M N P\) và \(A C B\) cũng không đồng dạng với nhau.

Ta có \(\frac{A B}{C D}=\frac{4}{6}=\frac{2}{3} ; \mathrm{CH}=\mathrm{AC}+\mathrm{AH}=1+2=3\) nên \(\frac{A H}{C H}=\frac{2}{3}\).
Xét hai tam giác \(A B H\) vuông tại \(H\) và tam giác \(C D H\) vuông tại \(H\) có:
\(\frac{A B}{C D}=\frac{A H}{C H}=\frac{2}{3} \text {. }\)

Do đó \(\triangle \mathrm{ABH} \backsim \triangle \mathrm{CDH}\).
Suy ra \(\widehat{A B D}=\widehat{A B H}=\widehat{C D H}=\widehat{C D B}\). vậy \(\widehat{A B D}=\widehat{C D B}\).

- Gọi chiều ngang của chiếc ti vi mới là x (m).

Xét hai tam giác vuông lần lượt có các cạnh góc vuông là hai cạnh (nằm ngang và thẳng đứng) của màn hình hai chiếc tivi 32 inch và 55 inch. Đường chéo của chúng có độ dài lần lượt là 32 inch và 55 inch. Hai tam giác vuông này đồng dạng với nhau vì có hai cặp cạnh góc vuông tỉ lệ. Do đó \(\frac{x}{72}=\frac{55}{32} \Rightarrow x=\frac{55 \cdot 72}{32}=123,75 \mathrm{~cm}=\) \(1,2375 \mathrm{~m}>1 \mathrm{~m}\).

Vậy không thể đặt vừa chiếc ti vi 55 inch vào khoảng trống hình vuông cạnh 1 m.

Các giả thiết a), b) và d) suy ra hai tam giác vuông đồng dạng, giả thiết c) không suy ra hai tam giác vuông đồng dạng.

+ Giả thiết a) suy ra hai tam giác vuông đồng dạng theo trường hợp góc – góc.

+ Giả thiết b) suy ra hai tam giác vuông đồng dạng theo trường hợp cạnh huyền – cạnh góc vuông.

+ Giả thiết d) suy ra hai tam giác vuông đồng dạng theo trường hợp cạnh – góc – cạnh.

+ Vì \(\frac{1}{1} \neq \frac{2}{4}\) nên cặp tam giác vuông ở hình a) không đồng dạng.
+ Độ dài cạnh góc vuông còn lại ở tam giác vuông có một cạnh bằng 1 ở hình b) là \(\sqrt{2^2-1^1}=\sqrt{3}\), khi đó \(\frac{\sqrt{3}}{1} \neq \frac{4}{2}\) nên cặp tam giác vuông ở hình b) không đồng dạng.
+ Tính số đo hai góc nhọn chưa biết trong hai hình vuông ở hình c) ta được kết quả là \(30^{\circ}\) và \(20^{\circ}\) nên cặp tam giác vuông ở hình c) không đồng dạng.
+ Cặp tam giác vuông ở hình d) đồng dạng với nhau. Vi cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia \(\left(\frac{1}{1,5}=\frac{3}{4,5}=\frac{2}{3}\right)\).

Xét hai tam giác vuông OBN (vuông tại N) và tam giác OAM (vuông tại M) có:
Góc nhọn \(\widehat{O}\) chung.
Suy ra \(\triangle \mathrm{OAM} \sim \triangle \mathrm{OBN}\).

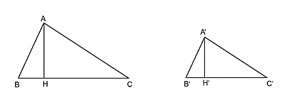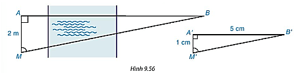
a) Ta có \(A C=3 A B\). Suy ra \(\frac{A B}{A C}=\frac{1}{3}\).
- Có \(B^{\prime} D^{\prime}=3 A^{\prime} B^{\prime}\). Suy ra \(\frac{A^{\prime} B^{\prime}}{B^{\prime} D^{\prime}}=\frac{1}{3}\).

Do đó, \(\frac{A B}{A C}=\frac{A^{\prime} B^{\prime}}{B^{\prime} D^{\prime}}\), suy ra \(\frac{A B}{A^{\prime} B^{\prime}}=\frac{A C}{B^{\prime} D^{\prime}}\).
Mà \(A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) là hình chữ nhật nên \(A^{\prime} C^{\prime}=B^{\prime} D^{\prime}\), do đó \(\frac{A B}{A^{\prime} B^{\prime}}=\frac{A C}{A^{\prime} C^{\prime}}\).
Xét tam giác vuông \(A B C\) (vuông tại \(B\) ) và tam giác vuông \(A^{\prime} B^{\prime} C^{\prime}\) (vuông tại \(B^{\prime}\) ) có \(\frac{A B}{A^{\prime} B^{\prime}}=\frac{A C}{A^{\prime} C^{\prime}}\).

Suy ra \(\triangle A B C \sim \triangle A^{\prime} B^{\prime} C^{\prime}\) (cạnh huyền - cạnh góc vuông).

b) Vì \(A^{\prime} B^{\prime}=2 A B\). Suy ra \(\frac{A B}{A^{\prime} B^{\prime}}=\frac{1}{2}\).

Mà \(\triangle A B C \backsim \triangle A^{\prime} B^{\prime} C^{\prime}\). Suy ra \(\frac{A C}{A^{\prime} C^{\prime}}=\frac{B C}{B^{\prime} C^{\prime}}=\frac{A B}{A^{\prime} B^{\prime}}=\frac{1}{2}\).
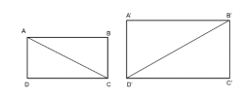
+ Ta có diện tích hình chữ nhật \(A B C D\) là: \(A B \cdot B C\)
+ Diện tích hình chữ nhật A'B'C'D' là: A'B' - B'C'.
Xét tỉ lệ diện tích hai hình chữ nhật \(A B C D\) và \(A^{\prime} B^{\prime} C^{\prime} D^{\prime}\), có
\(\frac{A B \cdot B C}{A^{\prime} B^{\prime} \cdot B C}=\frac{A B}{A^{\prime} B^{\prime}} \cdot \frac{B C}{B^{\prime} C^{\prime}}=\frac{1}{2} \cdot \frac{1}{2}=\frac{1}{4} .\)

Suy ra \(A^{\prime} B^{\prime} \cdot B^{\prime} C^{\prime}=4 A B \cdot B C=4 \cdot 2=8 \mathrm{~m}^2\).
Vậy diện tích hình chữ nhật A'B'C'D' là 8 m².

a) Vì \(\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle A B C\) theo tỉ số k nên \(\widehat{B}=\widehat{B^{\prime}} ; \quad \frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{B^{\prime} C^{\prime}}{B C}=k\).

Xét tam giác A'H'B' vuông tại H' và tam giác AHB vuông tại \(H\) có: \(\widehat{B}=\widehat{B^{\prime}}\).
Do đó \(\triangle A^{\prime} H^{\prime} B^{\prime} \backsim \triangle A H B\).
Suy ra \(\frac{A^{\prime} H^{\prime}}{A H}=\frac{A^{\prime} B^{\prime}}{A B}=k\).

b) Diện tích tam giác \(\mathrm{ABC}\) là \(\frac{1}{2} \cdot A H \cdot B C\)

Diện tích tam giác \(A^{\prime} B^{\prime} C^{\prime}\) là \(\frac{1}{2} \cdot A^{\prime} H^{\prime} \cdot B^{\prime} C^{\prime}\)
Xét tỉ lệ diện tích giữa hai tam giác \(A^{\prime} B^{\prime} C^{\prime}\) và tam giác \(A B C\) :
\(\frac{\frac{1}{2} A^{\prime} H^{\prime} \cdot B^{\prime} C^{\prime}}{\frac{1}{2} A H \cdot B C}=\frac{A^{\prime} H^{\prime}}{A H} \cdot \frac{B^{\prime} C^{\prime}}{B C}=k \cdot k=k^2 \text { Suy ra } \frac{1}{2} A^{\prime} H^{\prime} \cdot B^{\prime} C^{\prime}=k^2 \cdot \frac{1}{2} A H \cdot B C \text {. }\)

Vậy diện tích tam giác \(A^{\prime} B^{\prime} C^{\prime}\) bằng k k lần diện tích tam giác \(A B C\).

Ta có \(\mathrm{A}^{\prime} \mathrm{M}^{\prime}=1 \mathrm{~cm}=0,01 \mathrm{~m} ; \mathrm{A}^{\prime} \mathrm{B}^{\prime}=5 \mathrm{~cm}=0,05 \mathrm{~m}\).
Xét \(\triangle \mathrm{A}^{\prime} \mathrm{M}^{\prime} \mathrm{B}^{\prime}\) (vuông tại \(\mathrm{A}^{\prime}\) ) và \(\triangle \mathrm{AMB}\) (vuông tại \(\mathrm{A}\) ) có \(\widehat{A}^{\prime} \widehat{M^{\prime} B^{\prime}}=\widehat{A M B}\) (giả thiết).
Do đó, \(\triangle \mathrm{A}^{\prime} \mathrm{M}^{\prime} \mathrm{B}^{\prime} \sim \triangle \mathrm{AMB}\).
Suy ra \(\frac{A^{\prime} M^{\prime}}{A M}=\frac{A^{\prime} B^{\prime}}{A B}\) hay \(\frac{0,01}{2}=\frac{0,05}{A B}\). Suy ra \(A B=\frac{0,05 \cdot 2}{0,01}=10(\mathrm{~m})\).
Vậy khoảng cách từ \(A\) đến \(B\) là 10 m.