Mở đầu
93
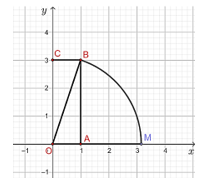
Bạn Lan vẽ một hình chữ nhật với chiều rộng và chiều dài lần lượt là 1; 3 (đơn vị độ dài). Sau đó Lan đặt lên trục số đoạn OM có độ dài bằng độ dài của đường chéo hình chữ nhật vừa vẽ (trục số nằm ngang và M nằm bên phải gốc O). Hỏi điểm M biểu diễn số thực nào? Biết rằng đơn vị độ dài trên trục số và đơn vị độ dài đo kích thước hình chữ nhật là như nhau.
Đáp án
Để biết được điểm M biểu diễn số thực nào, ta cần tính độ dài đoạn thẳng OM, hay chính là tính độ dài đường chéo OB của hình chữ nhật OABC khi biết chiều dài và chiều rộng của hình chữ nhật đó, điều này dẫn đến việc cần tính độ dài cạnh huyền của tam giác vuông khi biết độ dài hai cạnh góc vuông. Để làm được điều này, ta sẽ sử dụng kiến thức của bài học hôm nay.