Bài 34: Ba trường hợp đồng dạng của hai tam giác

Vì trong hình vẽ mặt sân được vẽ nghiêng nên nếu đo trực tiếp trong sách giáo khoa sẽ không đúng bằng góc thực tế.

Vẽ một tam giác bằng dụng cụ học tập trên giấy có một góc đúng bằng góc sút. Từ đó sử dụng dụng cụ học tập là thước đo góc để đo góc sút.

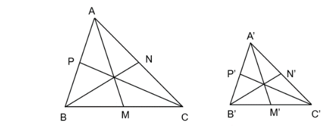
a) Nếu $\mathrm{A}^{\prime} \mathrm{B}^{\prime}=\mathrm{AB}$ thì từ $\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{B^{\prime} C^{\prime}}{B C}$, suy ra $\mathrm{A}^{\prime} C^{\prime}=\mathrm{AC}$ và $\mathrm{B}^{\prime} \mathrm{C}^{\prime}=\mathrm{BC}$.

Do đó $\triangle A B C=\triangle A^{\prime} B^{\prime} C^{\prime}$ (c.c.c). Vậy $\triangle A B C \sim \triangle A^{\prime} B^{\prime} C^{\prime}$.

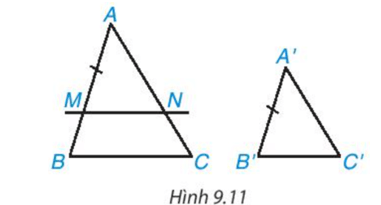
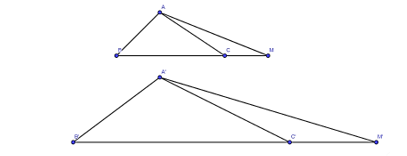
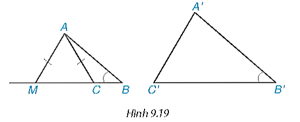
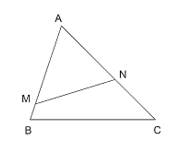
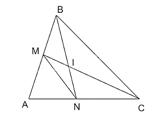
b) Ta có $M N / / B C(M \in A B, N \in A C)$. Suy ra $\triangle A M N \sim \triangle A B C$.

Suy ra $\frac{A M}{A B}=\frac{A N}{A C}=\frac{M N}{B C}$.
Mà $\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{B^{\prime} C^{\prime}}{B C}$ nên $\frac{A^{\prime} B^{\prime}}{A M}=\frac{A^{\prime} C^{\prime}}{A N}=\frac{B^{\prime} C^{\prime}}{M N}$.
Có $A M=A^{\prime} B^{\prime}$, suy ra $A^{\prime} C^{\prime}=A N$ và $B^{\prime} C^{\prime}=M N$ nên $\triangle A M N=\Delta A^{\prime} B^{\prime} C^{\prime}$ (c.c.c).
Suy ra $\triangle A M N \backsim \triangle A^{\prime} B^{\prime} C^{\prime}$, mà $\triangle A M N \backsim \triangle A B C$ nên $\triangle A B C \backsim \triangle A^{\prime} B^{\prime} C^{\prime}$.

c) Nếu $A^{\prime} B^{\prime}>A B$, bằng cách đổi vai trò cho $\triangle A B C$ và $\triangle A^{\prime} B^{\prime} C^{\prime}$ cho nhau thì theo câu b), ta có $\triangle \mathrm{ABC} \sim \triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime}$.

Ta có $\triangle \mathrm{ABC} \sim \Delta \mathrm{HGK}$ (c.c.c) vì $\frac{A B}{H G}=\frac{B C}{G K}=\frac{A C}{H K}=\frac{1}{2}$.

Ta có $\triangle \mathrm{DEF} \sim \Delta \mathrm{MNP}$ (c.c.c) vì $\frac{D E}{M N}=\frac{E F}{N P}=\frac{D F}{M P}=\frac{1}{2}$.

Vì chu vi tam giác $A B C$ bằng $18 \mathrm{~cm}$.
Suy ra $A B+A C+B C=18$. Suy ra $4+A C+6=18$ nên $A C=8(c m)$.
Vi chu vi tam giác DEF bằng $27 \mathrm{~cm}$.
Suy ra $D E+E F+D F=27$. Suy ra $6+E F+12=27$ nên $E F=9(c m)$
Ta thấy: $\frac{A B}{D E}=\frac{A C}{D F}=\frac{B C}{E F}=\frac{4}{6}=\frac{8}{12}=\frac{6}{9}=\frac{2}{3}$.
Suy ra $\triangle A B C \sim \triangle D E F$ (c.c.c).

Có thể vẽ tam giác $A B C$ có các cạnh lần lượt bằng $2 \mathrm{~cm} ; 3 \mathrm{~cm} ; 4 \mathrm{~cm}$ sau đó xét các tỉ lệ ta thấy $\frac{7,32}{2}=\frac{10,98}{3}=\frac{14,64}{4}=3,66$ nên tam giác $A B C$ đồng dạng với tam giác tạo bởi ba đỉnh là trái bóng và hai chân cột gôn.

Lấy thước đo góc để đo các góc của tam giác từ đó tính được góc sút.
Ta đo được góc sút bằng khoảng $29^{\circ}$.

- Ta có: $\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{3}{2}$.
- Đo được $\mathrm{BC} \approx 2,6 \mathrm{~cm} ; \mathrm{B}^{\prime} \mathrm{C}^{\prime} \approx 3,9 \mathrm{~cm}$.

Tỉ số $\frac{B^{\prime} C^{\prime}}{B C}=\frac{3}{2}$. Do đó $\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{B^{\prime} C^{\prime}}{B C}$.
- Vậy $\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle A B C$ (c.c.c) với tỉ số đồng dạng là $\frac{3}{2}$.

Ta có: $\triangle \mathrm{ACB} \backsim \triangle \mathrm{MPN}$ vì $\widehat{A}=\widehat{M}=70^{\circ}$ và $\frac{A C}{M P}=\frac{A B}{M N}=\frac{1}{2}$

Có $\frac{M C}{M B}=\frac{M^{\prime} C^{\prime}}{M^{\prime} B^{\prime}}$. Suy ra $\frac{M B-B C}{M B}=\frac{M^{\prime} B^{\prime}-B^{\prime} C^{\prime}}{M^{\prime} B^{\prime}}$
Suy ra $1-\frac{B C}{M B}=1-\frac{B^{\prime} C^{\prime}}{M^{\prime} B^{\prime}}$. Do đó, $\frac{B C}{M B}=\frac{B^{\prime} C^{\prime}}{M^{\prime} B^{\prime}}$, suy ra $\frac{B^{\prime} C^{\prime}}{B C}=\frac{M^{\prime} B^{\prime}}{M B}$.
Vi $\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle A B C$. Suy ra $\widehat{B}=\widehat{B^{\prime}}$ và $\frac{A^{\prime} B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C}$. (2)
Từ (1) và (2) suy ra $\frac{M^{\prime} B^{\prime}}{M B}=\frac{A^{\prime} B^{\prime}}{A B}$.
Xét tam giác $A B M$ và tam giác $A^{\prime} B^{\prime} M^{\prime}$ có:
$\frac{M^{\prime} B^{\prime}}{M B}=\frac{A^{\prime} B^{\prime}}{A B}$ và $\widehat{B}=\widehat{B^{\prime}}$ (chứng minh trên).
Do đó $\triangle A B M \backsim \triangle A^{\prime} B^{\prime} M^{\prime}$ (c.g.c).

Bạn Lan nhận xét không đúng.
Ví dụ lấy $\triangle \mathrm{ABM} \sim \Delta \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime}$ với $\widehat{C^{\prime}}=\widehat{M}<90^{\circ}$ và lấy $\mathrm{C}$ trên đoạn $\mathrm{MB}$ sao cho $\triangle \mathrm{AMC}$ cân tại $A$ như H.9.19 thì $\triangle A B C$ và $\triangle A^{\prime} B^{\prime} C^{\prime}$ không đồng dạng.

Dự đoán: Hai tam giác có hình dạng rất giống nhau chỉ khác về kích thước nên chúng có khả năng đồng dạng với nhau. Khi đó tỉ số đồng dạng bằng $\frac{A^{\prime} B^{\prime}}{A B}=\frac{2}{1000}=\frac{1}{500}$.
$\left(A B=10 m=1000 \mathrm{~cm}, A^{\prime} B^{\prime}=2 c m\right)$

Nếu $\triangle A^{\prime} B^{\prime} C^{\prime} \backsim \triangle \mathrm{ABC}$ thì $\frac{A^{\prime} C^{\prime}}{A C}=\frac{A^{\prime} B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C}$.
Mà $\mathrm{A}^{\prime} \mathrm{C}^{\prime} \quad=\quad 3,76 \mathrm{~cm}$ và $\frac{A^{\prime} C^{\prime}}{A C}=\frac{A^{\prime} B^{\prime}}{A B} \quad$ suy ra $A C=\frac{A^{\prime} C^{\prime}}{A^{\prime} B^{\prime}} . A B=\frac{3,76: 100}{2: 100} \cdot 10=18,8(\mathrm{~m})$

Xét tam giác MPN có:
$\widehat{P}=180^{\circ}-\widehat{M}-\widehat{N}=180^{\circ}-60^{\circ}-70^{\circ}=50^{\circ} \text {. }$

Các cặp tam giác đồng dạng trong Hình 9.22 là:
+) $\triangle \mathrm{ACB} \sim \triangle \mathrm{DFE}$ (g.g) vì $\widehat{A}=\widehat{D}=60^{\circ} ; \widehat{B}=\widehat{E}=50^{\circ}$.
+) $\triangle \mathrm{ACB} \sim \triangle \mathrm{MNP}$ (g.g) vì $\widehat{A}=\widehat{M}=60^{\circ} ; \widehat{B}=\widehat{P}=50^{\circ}$.
+) $\triangle \mathrm{DEF} \sim \triangle \mathrm{MPN}$ (g.g) vì $\widehat{D}=\widehat{M}=60^{\circ} ; \widehat{E}=\widehat{P}=50^{\circ}$.

Xét tam giác $A B C$ và tam giác $A D B$ có:
$\widehat{A B C}=\widehat{A D B}$ và $\widehat{A}$ chung
Do đó $\triangle A B C \backsim \triangle A D B$ (g.g).
Suy ra $\frac{A B}{A D}=\frac{A C}{A B}$, do đó $\mathrm{AB} \cdot \mathrm{AB}=\mathrm{AD} \cdot \mathrm{AC}$ hay $\mathrm{AB}^2=\mathrm{AD} \cdot \mathrm{AC}$.

1.

Do tổng các góc trong một tam giác bằng $180^o$ nên:

$\frac{\widehat{A^{\prime}}+\widehat{B^{\prime}}}{2}=180^{\circ}-\widehat{A^{\prime} I^{\prime} B^{\prime}}=180^{\circ}-\widehat{A I B}=\frac{\widehat{A}+\widehat{B}}{2} .$

Suy ra $\widehat{A^{\prime}}+\widehat{B^{\prime}}=\widehat{A}+\widehat{B}$. Do đó $\widehat{C^{\prime}}=180^{\circ}-\widehat{A^{\prime}}-\widehat{B^{\prime}}=180^{\circ}-\widehat{A}-\widehat{B}=\widehat{C}$. Tương tự ta có $\widehat{B}=\widehat{B^{\prime}}$. Vậy tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ có: $\widehat{B}=\widehat{B^{\prime}} ; \widehat{C}=\widehat{C^{\prime}}$.

Do đó $\triangle A B C \backsim \triangle A^{\prime} B^{\prime} C^{\prime}$ (g.g).
2. Nếu góc $C$ và góc $C^{\prime}$ đều nhọn, lấy điểm $M$ trên tia $B C$ sao cho $\triangle A B M \sim \triangle A^{\prime} B^{\prime} C^{\prime}$.

Giả sử điểm $\mathrm{C}$ không trùng với $\mathrm{M}$.
Khi đó $\triangle \mathrm{ABM} \backsim \triangle \mathrm{A}^{\prime} B^{\prime} C^{\prime}$ nên $\frac{A^{\prime} C^{\prime}}{A M}=\frac{A^{\prime} B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B M}$.
Mà $\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} C^{\prime}}{A C}$ (gt) nên $\frac{A^{\prime} C^{\prime}}{A M}=\frac{A^{\prime} C^{\prime}}{A C}$, suy ra $\mathrm{AC}=\mathrm{AM}$ hay $\triangle \mathrm{AMC}$ cân tại $\mathrm{A}$.
+) Nếu $\mathrm{M}$ nằm giữa $\mathrm{B}$ và $\mathrm{C}$ thì
$\widehat{A M B}=180^{\circ}-\widehat{A M C}=180^{\circ}-\widehat{A C M}>90^{\circ}>\widehat{C^{\prime}} \text { (Vô lí). }$
+) Nếu C nằm giữa $B$ và $M$ (như Hình 9.19). Khi đó
$\widehat{A C B}=180^{\circ}-\widehat{A C M}=180^{\circ}-\widehat{A M B}=180^{\circ}-\widehat{C^{\prime}}>90^{\circ} \text { (Vô lí). }$

Vậy điểm $C$ phải trùng với $M$ và $\triangle A B C \backsim \triangle A^{\prime} B^{\prime} C^{\prime}$.

Giả thiết a) suy ra hai tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh.

Giả thiết c) suy ra hai tam giác đồng dạng theo trường hợp góc – góc.

Các giả thiết b) và d) không suy ra hai tam giác đồng dạng.

Vì $6+12+15=33(\mathrm{~cm})$ và $\frac{4}{6}=\frac{8}{12}=\frac{10}{15}$ nên bộ ba trong câu a) là độ dài ba cạnh của tam giác thỏa mãn yêu cầu. Các bộ ba còn lại hoặc không có tổng bằng $33 \mathrm{~cm}$ hoặc không có tỉ lệ tương ứng với $(4: 8: 10)$ nên không thể là độ dài ba cạnh của tam giác thỏa mãn yêu cầu.

Vì $\triangle \mathrm{A}^{\prime} B^{\prime} C^{\prime} \sim \triangle \mathrm{ABC}$ nên: $\frac{A^{\prime} B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{A^{\prime} C^{\prime}}{A C}$; (1)
và $\widehat{A^{\prime} B^{\prime} C^{\prime}}=\widehat{A B C} ; \widehat{B^{\prime} C^{\prime} A}=\widehat{B C A} ; \widehat{C^{\prime} A^{\prime} B^{\prime}}=\widehat{C A B}$.
Hai tam giác A'B'M' và ABM có:
$\begin{aligned}\frac{B^{\prime} M^{\prime}}{B M}=\frac{\frac{B^{\prime} C^{\prime}}{2}}{\frac{B C}{2}}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{B^{\prime} A^{\prime}}{B A} \text { (theo (1)); } \\\widehat{A^{\prime} B^{\prime} M^{\prime}}=\widehat{A^{\prime} B^{\prime} C^{\prime}}=\widehat{A B C}=\widehat{A B M} \text { (theo (2)). }\end{aligned}$

Do đó $\triangle \mathrm{A}^{\prime} \mathrm{M}^{\prime} \mathrm{B}^{\prime} \sim \triangle \mathrm{AMB}$ (c.g.c). Suy ra $\frac{A^{\prime} M^{\prime}}{A M}=\frac{A^{\prime} B^{\prime}}{A B}$
Tương tự $\triangle \mathrm{A}^{\prime} C^{\prime} P^{\prime} \backsim \triangle \mathrm{ACP}$ và $\frac{C^{\prime} P^{\prime}}{C P}=\frac{A^{\prime} C^{\prime}}{A C}$ (4).
$\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{N}^{\prime} \backsim \triangle \mathrm{ABN}$ và $\frac{B^{\prime} N^{\prime}}{B N}=\frac{A^{\prime} B^{\prime}}{A B}(5)$.
Từ (1), (3), (4) và (5) suy ra $\frac{A^{\prime} M^{\prime}}{A M}=\frac{B^{\prime} N^{\prime}}{B N}=\frac{C^{\prime} P^{\prime}}{C P}$.

Có $\mathrm{AB}=12 \mathrm{~cm}, \mathrm{AN}=8 \mathrm{~cm}$. Suy ra $\frac{A N}{A B}=\frac{8}{12}=\frac{2}{3}$. $\mathrm{AC}=15 \mathrm{~cm}, \mathrm{AM}=10 \mathrm{~cm}$. Suy ra $\frac{A M}{A C}=\frac{10}{15}=\frac{2}{3}$.

Suy ra $\frac{A N}{A B}=\frac{A M}{A C}$.
Xét hai tam giác $A B C$ và tam giác ANM có:
$\frac{A N}{A B}=\frac{A M}{A C}, \widehat{A}$ chung.
Do đó $\triangle A B C \backsim \triangle A N M$ (c.g.c).

a) Xét tam giác ABN và tam giác ACM:

$\widehat{A}$ chung, $\widehat{A B N}=\widehat{A C M}$ (giả thiết)
Suy ra $\triangle A B N \backsim \triangle A C M$ (g.g).
b) Vì $\triangle A B N \backsim \triangle A C M$ (chứng minh trên) nên $\widehat{A N B}=\widehat{A M C}$.

Lại có: $\widehat{A N B}+\widehat{C N B}=180^{\circ} ; \widehat{A M C}+\widehat{B M C}=180^{\circ}$ (kề bù), suy ra $\widehat{C N B}=\widehat{B M C}$.

Xét tam giác IBM và tam giác ICN có:
$\widehat{C N B}=\widehat{B M C}$ (cmt) và $\widehat{I B M}=\widehat{I C N}$ (do $\widehat{A B N}=\widehat{A C M}$ )
Suy ra $\triangle I B M \sim \triangle I C N$ (g.g).
Suy ra $\frac{I B}{I C}=\frac{I M}{I N}$. Suy ra $\mathrm{IB} . \mathrm{IN}=\mathrm{IC}$. IM.

Kí hiệu các điểm như hình vẽ trên.

Ta có: AB, EF, CD đôi một song song vì cùng vuông góc với BC (do dựng thẳng đứng).

Do đó ΔCEF ∽ ΔCAB và ΔBEF ∽ ΔBDC.

Suy ra $\frac{E F}{A B}=\frac{C F}{C B}$ và $\frac{E F}{C D}=\frac{B F}{B C}$.
Do đó: $\frac{E F}{C D}+\frac{E F}{A B}=\frac{B F}{B C}+\frac{C F}{C B}=\frac{B F+C F}{B C}=\frac{B C}{B C}$.
Suy ra $\frac{E F(A B+C D)}{C D \cdot B A}=1$.
Vậy $h=E F=\frac{C D \cdot A B}{A B+C D}=\frac{2 \cdot 3}{3+2}=\frac{6}{5}=1,2$ (m).