Bài 33: Hai tam giác đồng dạng

Quan sát thấy \(C D\) và \(A B\) song song với nhau.
Sử dụng định lí Thalès, ta nhận xét về hai tỉ lệ \(\frac{E D}{E A}\) và \(\frac{E C}{E B}\).
Từ đó tìm ra tỉ số giữa các cạnh đế tính chiều cao cột đèn.

Ta thấy \(\frac{A B}{D E}=2 ; \frac{B C}{E F}=2 ; \frac{A C}{D F}=2\).

Ta có \(\triangle \mathrm{ABC} \sim \triangle \mathrm{DEF}\) với tỉ số đồng dạng \(\frac{B C}{E F}=\frac{12}{6}=2\).
Nhìn hình vẽ ta thấy tam giác GHK vuông tại G nên không thể đồng dạng với hai tam giác còn lại.

a) Tam giác \(A B C\) cân tại \(\mathrm{A}\) nên \(\widehat{B}=\widehat{C}\). (1)

Vì \(\triangle \mathrm{ABC} \sim \triangle \mathrm{MNP}\) nên \(\widehat{A}=\widehat{M} ; \widehat{B}=\widehat{N} ; \widehat{C}=\widehat{P}\). (2)
Từ (1) và (2) suy ra \(\widehat{N}=\widehat{P}\) suy ra tam giác MNP cân tại \(\mathrm{M}\).

b) Vì tam giác \(A B C\) đều nên \(\widehat{A}=\widehat{C}=\widehat{B}=60^{\circ}\). (3)

Từ (1) và (3) suy ra \(\widehat{M}=\widehat{N}=\widehat{P}=60^{\circ}\) nên tam giác MNP là tam giác đều.

c) Vì tam giác \(A B C\) có \(A B \geq A C \geq B C\) suy ra \(\widehat{C} \geq \widehat{B} \geq \widehat{A}\) (quan hệ giữa góc và cạnh đối diện trong một tam giác). (4)
Từ (2) và (4) suy ra \(\widehat{P} \geq \widehat{N} \geq \widehat{M}\) nên \(M N \geq M P \geq N P\).

- Các cặp góc bằng nhau của hai tam giác ABC và AMN:
\(\widehat{B}=\widehat{A M N} ; \widehat{C}=\widehat{A N M}\) (do \(\mathrm{MN} / / \mathrm{BC}\) và các cặp góc này ở vị trí đồng vị);
\(\widehat{A}\) chung.
- Có MN // BP (vì MN // BC), MB // NP (vì \(A B / / N P\) ) nên MNPB là hình bình hành.

Suy ra \(\mathrm{MN}=\mathrm{BP}\). Suy ra \(\frac{M N}{B C}=\frac{B P}{B C}=\frac{A N}{A C}=\frac{A M}{A B}\) (Sử dụng định lí Thalès).
- Có \(\widehat{B}=\widehat{A M N} ; \widehat{C}=\widehat{A N M} ; \widehat{A}\) chung và \(\frac{A M}{A B}=\frac{A N}{A C}=\frac{M N}{B C}\), suy ra \(\triangle \mathrm{ABC} \backsim \triangle \mathrm{AMN}\).

- Vì C ∊ OA, D ∊ OB và CD //AB nên ∆OCD ∽ ∆OAB.

- Vì E ∊ OB, F ∊ OA (thuộc phần kéo dài) và EF // AB nên ∆OEF ∽ ∆OBA.

- Vì F ∊ OC, E ∊ OD (thuộc phần kéo dài) và EF // CD nên ∆OEF ∽ ∆ODC.

Có \(E B=4 \mathrm{~m}=400 \mathrm{~cm}, C D=1 \mathrm{~m}=100 \mathrm{~cm}\).
Vi cọc gỗ và cột đèn đều thẳng đứng. Suy ra \(\mathrm{AB} / / \mathrm{DC}\). Do đó, \(\triangle \mathrm{AEB} \sim \triangle \mathrm{EDC}\). Suy ra \(\frac{D E}{A E}=\frac{C E}{B E}=\frac{D C}{A B}\). Mà \(\frac{C E}{B E}=\frac{80}{400}=\frac{1}{5}\).

Vậy hai tam giác AEB và EDC đồng dạng với tỉ số \(\frac{1}{5}\).
Do đó, \(\frac{D C}{A B}=\frac{100}{A B}=\frac{1}{5}\). Suy ra \(A B=500 \mathrm{~cm}=5 \mathrm{~m}\).
Vậy chiều cao cột đèn là 5 m.

Từ giả thiết ta thấy ∆ABC và ∆MNP đồng dạng với các cặp đỉnh tương ứng là A tương ứng M, B tương ứng N, C tương ứng P. Do đó các khẳng định a), b), c) đúng và khẳng định d) không đúng (do nếu viết theo d thì đỉnh C tương ứng với đỉnh N, đỉnh B tương ứng với đỉnh P).

+ Khẳng định a là khẳng định đúng vì các tam giác bằng nhau thì các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên tỉ số giữa các cạnh tương ứng bằng nhau nên theo định nghĩa hai tam giác đồng dạng thì hai tam giác bằng nhau thì đồng dạng với nhau.

+ Khẳng định c là khẳng định đúng vì tam giác đều thì có các góc bằng 60° và các cạnh bằng nhau nên ta suy ra các góc tương ứng của hai tam giác đều bất kì bằng nhau và tỉ số các cạnh tương ứng của hai tam giác đều bất kì bằng nhau.

+ Khẳng định b sai vì hai tam giác gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau từng đôi một và ba cặp cạnh tương ứng tỉ lệ.

+ Khẳng định d sai vì hai tam giác vuông mới chỉ thỏa mãn một điều kiện để xét đồng dạng, cần thêm tỉ lệ cạnh tương ứng hoặc 1 góc tương ứng bằng nhau.

+ Khẳng định e sai vì hai tam giác đồng dạng chỉ có kích thước tỉ lệ với nhau, còn hai tam giác bằng nhau là có các góc, các cạnh tương ứng bằng nhau.

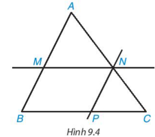
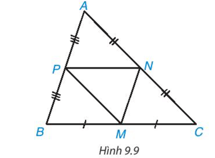
- Do N, P lần lượt là trung điểm của CA, AB.

Suy ra PN là đường trung bình của tam giác ABC nên NP // BC (P ∈ AB, N ∈ AC).

Suy ra ΔABC ∽ ΔAPN. 

- Do M, P lần lượt là trung điểm của BC, AB.

Suy ra MP là đường trung bình của tam giác ABC nên MP // AC (P ∈ AB, M ∈ BC)

Suy ra ΔABC ∽ ΔPBM.

- Do M, N lần lượt là trung điểm của BC, AC.

Suy ra MN là đường trung bình của tam giác ABC nên MN // AB (N ∈ AC, M ∈ BC).

Suy ra ΔABC ∽ ΔNMC.

- Ta có \(\widehat{A}=\widehat{B P M}\) (do \(\triangle \mathrm{ABC} \sim \triangle \mathrm{PBM}\) ); \(\widehat{A P N}=\widehat{B}\) (do \(\mathrm{PN} / / \mathrm{BC}\) ); \(\widehat{A N P}=\widehat{P M B}\) (do cùng bằng góc C); \(\frac{A P}{P B}=\frac{A N}{P M}=\frac{P N}{B M}=1\).

Do đó, \(\triangle \mathrm{APN} \backsim \triangle \mathrm{PBM}\).
- Tương tự ta cũng có \(\triangle \mathrm{NMC} \sim \triangle \mathrm{PBM}\).
- Ta có \(\triangle \mathrm{APN}=\triangle \mathrm{MNP}(\mathrm{g}-\mathrm{c}-\mathrm{g})\) vì \(\widehat{A P N}=\widehat{M N P} ; \widehat{A N P}=\widehat{M P N}\) (NP // BC và các cặp góc ở vị trí so le trong) và PN cạnh chung. Do đó \(\triangle A P N \backsim \triangle M N P\).

Vậy ta có 5 tam giác APN, PBM, NMC, MNP, ABC đôi một đồng dạng với nhau.

Vì tam giác \(A B C\) cân tại A nên \(\widehat{A B C}=\widehat{A B C}=\frac{\widehat{A B C}+\widehat{A C B}}{2}=\frac{180^{\circ}-\widehat{B A C}}{2}\).
Tương tự, tam giác MNP cân tại \(\mathrm{M}\) nên \(\widehat{M N P}=\frac{180^{\circ}-\widehat{P M N}}{2}\)
vì \(\widehat{B A C}=\widehat{P M N}\) nên từ (1) và (2) suy ra \(\widehat{A B C}=\widehat{M N P}\).
Lấy \(B^{\prime}, C^{\prime}\), lần lượt là trung điếm của \(A B, A C\) thì ta có \(B^{\prime} C^{\prime} / / B C\).
Do đó \(\widehat{A B C}=\widehat{A B^{\prime} C}\) ' \(\widehat{A C B}=\widehat{A C^{\prime} B}\) ' (các cặp góc đồng vị).
Hai tam giác \(A B^{\prime} C^{\prime}\) và MNP có:

\(\widehat{B^{\prime} A C}=\widehat{N M P}\) (theo giả thiết);
\(A B^{\prime}=\frac{A B}{2}=M N\) (theo giả thiết);
\(\widehat{A B^{\prime} C^{\prime}}=\widehat{A B C}=\widehat{M N P} \backslash\) (chứng minh trên).
Vậy \(\triangle M N P=\Delta A B^{\prime} C^{\prime}\) (g.c.g).
Mặt khác, \(\triangle \mathrm{AB}^{\prime} \mathrm{C}^{\prime} \backsim \triangle \mathrm{ABC}\) (vì \(\mathrm{B}^{\prime} \mathrm{C}^{\prime} / / \mathrm{BC}\) ).
Do đó, \(\triangle \mathrm{MNP} \sim \triangle \mathrm{ABC}\) với tỉ số đồng dạng \(k=\frac{M N}{A B}=\frac{A B}{A B}=\frac{1}{2}\).