Mở đầu
40
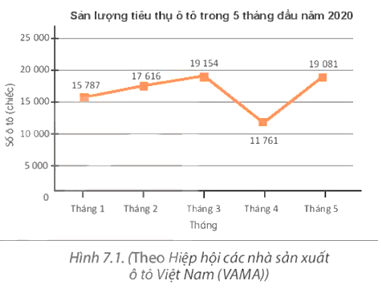
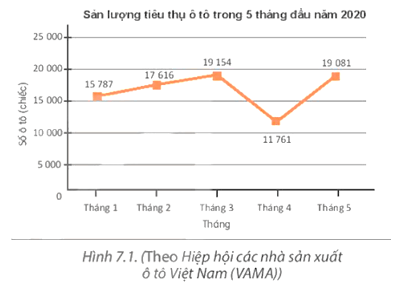
Hình 7.1 là biểu đồ đoạn thẳng mô tả sản lượng tiêu thụ ô tô của thị trường Việt Nam trong 5 tháng đầu năm 2020. Em hãy cho biết trong tháng nào thì số lượng ô tô tiêu thụ là ít nhất.
Đáp án
Quan sát biểu đồ ta thấy tháng 4 là tháng số lượng ô tô tiêu thụ ít nhất.