Mở đầu
81
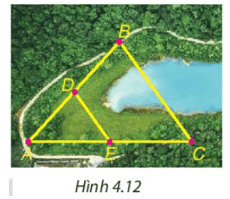
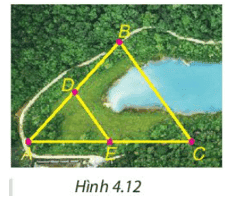
Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
Đáp án
Sau bài học này ta giải quyết được bài toán như sau:
Trong tam giác \(A B C\) có \(D, E\) lần lượt là trung điểm của \(A B\) và \(A C\) nên \(D \in A B ; E \in\) \(A C\) và \(A D=B D ; A E=E C\).
Suy ra DE là đường trung bình của tam giác \(\mathrm{ABC}\).
Do đó \(D E=\frac{1}{2} B C\) suy ra \(\mathrm{BC}=2 \mathrm{DE}=2.500=1000(\mathrm{~m})\)
Vậy khoảng cách giữa hai điểm \(B\) và C bằng \(1000 \mathrm{~m}\).