Mở đầu
76
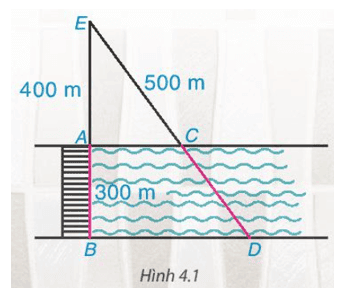
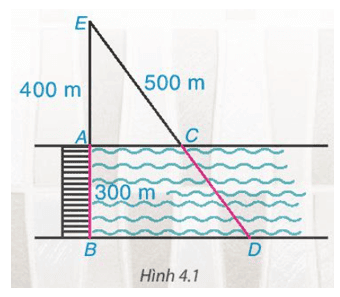
Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào?
Đáp án
Sau bài học này ta giải quyết được bài toán như sau:
Hai cạnh \(A C\) và \(B D\) thuộc hai bờ của con sông nên \(A C / / B D\), áp dụng định lí Thalès, ta có:
\(\frac{A E}{A B}=\frac{C E}{C D}\) hay \(\frac{400}{300}=\frac{500}{C D}\).
Suy ra \(C D=\frac{300 \cdot 500}{400}=375(\mathrm{~m})\)
Vậy khoảng cách giữa C và D bằng 375 m.