Câu hỏi 1
67
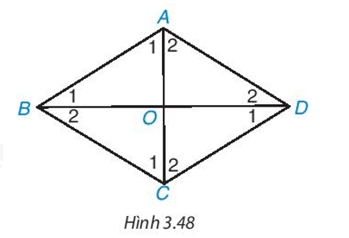
Hình thoi có phải là hình bình hành không? Nếu có, từ tính chất đã biết của hình bình hành, hãy suy ra những tính chất tương ứng của hình thoi.
Gợi ý
Dựa vào định nghĩa hình thoi
Đáp án
Hình thoi có bốn cạnh bằng nhau nên ta suy ra hai cặp cạnh đối bằng nhau.
Ta suy ra tính chất hình thoi dựa vào tính chất của hình bình hành như sau:
- Hình thoi có hai góc đối bằng nhau.
- Hình thoi có các cặp cạnh đối song song.
- Hình thoi có hai đường chéo cắt nhau tại trung điểm của mỗi đường.