Hoạt động 1
64
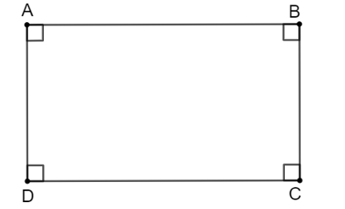
Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao?
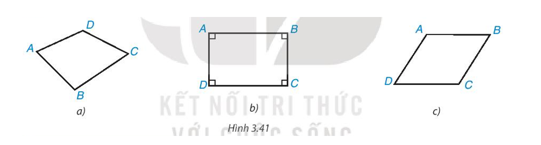
Gợi ý
Quan sát hình 3.41
Đáp án
Tứ giác \(A B C D\) trong Hình \(3.41 \mathrm{~b}\) là hình chữ nhật vì có
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^{\circ}\)
Tứ giác \(A B C D\) trong Hình 3.41 a và Hình \(3.41 c\) không phải là hình chữ nhật vì không có 4 góc vuông.