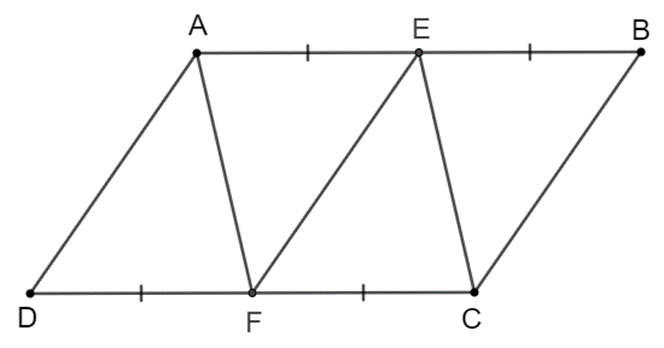
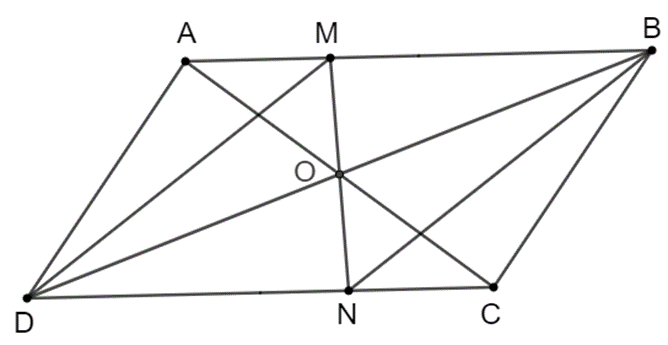
Hoạt động 1
57
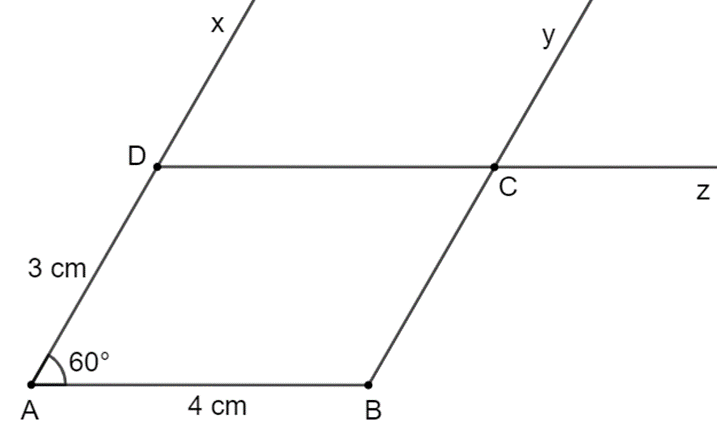
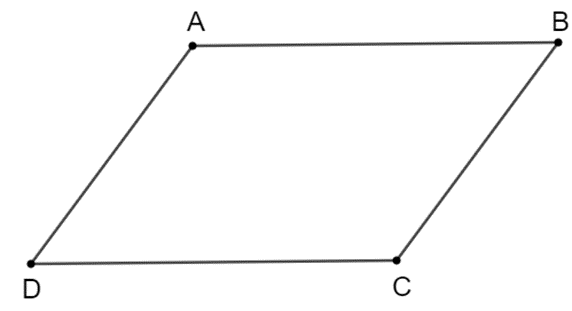
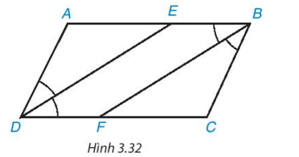
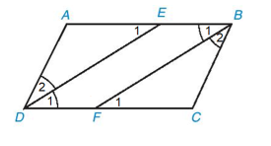
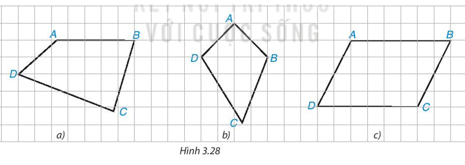
Trong Hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?
Gợi ý
Quan sát hình 3.28
Đáp án
Tứ giác trong Hình 3.28c là hình bình hành vì:
Ta so sánh độ dài các cạnh đối trong tứ giác bằng cách đếm số ô vuông trong hình.
Ta thấy AB = CD; AD = BC.