Luyện tập 1
53
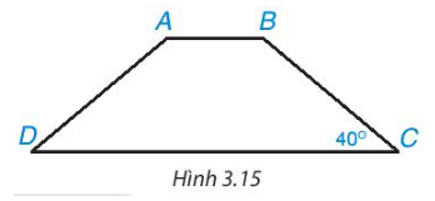
Tính các góc của hình thang cân \(\mathrm{ABCD}(\mathrm{AB} / / \mathrm{CD})\), biết \(\widehat{C}=40^{\circ}(\mathrm{H} .3 .15)\).
Gợi ý
Sử dụng tính chất của hình thang cân và áp dụng định lí tổng các góc trong một tứ giác.
Đáp án
Hình thang cân \(A B C D(A B / / C D)\) nên ta có:
\(\begin{aligned}\widehat{A}=\widehat{B} ; \widehat{C}=\widehat{D}=40^{\circ} \\ \widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{\circ}\end{aligned}\)
Khi đó: \(\widehat{A}+\widehat{A}+40^{\circ}+40^{\circ}=360^{\circ}\)
Hay: \(2 \widehat{A}+80^{\circ}=360^{\circ}\)
Suy ra: \(2 \widehat{A}=360^{\circ}-80^{\circ}=280^{\circ}\)
Do đó: \(\widehat{A}=140^{\circ}\) nên \(\widehat{B}=140^{\circ}\)
Vậy: \(\widehat{A}=140^{\circ} ; \widehat{B}=140^{\circ} ; \widehat{C}=40^{\circ} ; \widehat{D}=40^{\circ}\)