Bài 10: Tứ giác

- Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Khi đó: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{\circ}\) (phần này sẽ được tìm hiểu ở mục 2, trang 50 SGK Toán 8 - Tập 1).

Nối EG, GF, FH, HE, ta được tứ giác EGFH như hình vẽ.

– Đường chéo còn lại của tứ giác ABCD là BD.

– Cặp cạnh đối còn lại của tứ giác ABCD là cặp cạnh AD và BC.

– Cặp góc đối còn lại của tứ giác ABCD là cặp góc B và D.

Áp dụng định lí về tổng ba góc trong một tam giác đối với tam giác \(A B D\) và \(C B D\), ta có:
\(\begin{aligned}& \widehat{A}+\widehat{B}_1+\widehat{D}_1=180^{\circ} \\& \widehat{C}+\widehat{B}_2+\widehat{D}_2=180^{\circ}\end{aligned}\)
Khi đó, tứ giác \(A B C D\) có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=\widehat{A}+\widehat{B}_1+\widehat{D}_1+\widehat{C}+\widehat{B}_2+\widehat{D}_2=180^{\circ}+180^{\circ}=360^{\circ}\)
Vậy \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{\circ}\).

Xét tứ giác EFGH có:
\(\widehat{E}+\widehat{F}+\widehat{G}+\widehat{H}=360^{\circ}\) (định lí tổng các góc trong một tứ giác).
Hay \(90^{\circ}+\widehat{F}+90^{\circ}+55^{\circ}=360^{\circ}\)
Suy ra \(\widehat{F}+235^{\circ}=360^{\circ}\)
Do đó \(\widehat{F}=360^{\circ}-235^{\circ}=125^{\circ}\).
Vậy \(\widehat{F}=125^{\circ}\).

- Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Khi đó: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{\circ}\) (phần này sẽ được tìm hiểu ở mục 2, trang 50 SGK Toán 8 - Tập 1).

• Nếu 4 góc trong tứ giác đều nhọn (mỗi góc nhỏ hơn \(90^{\circ}\) ).
Khi đó, tổng 4 góc nhỏ hơn: \(4.90^{\circ}=360^{\circ}\) (vô lí vì tổng 4 góc trong tứ giác bằng \(360^{\circ}\) ).
- Nếu tứ giác có 3 góc nhọn (nhỏ hơn 90²); 1 góc tù (góc lớn hơn \(90^{\circ}\) ).
Khi đó, tổng 3 góc nhọn nhỏ hơn: \(3.90^{\circ}=270^{\circ}\);
Số đo góc còn lại lớn hơn: \(360^{\circ}-270^{\circ}=90^{\circ}\) (thỏa mãn).
Do đó, một tứ giác có thể có nhiều nhất 3 góc nhọn.
• Nếu 4 góc tứ giác đều tù (mỗi góc lớn hơn \(90^{\circ}\) ).
Khi đó, tổng 4 góc lớn hơn: \(4.90^{\circ}=360^{\circ}\) (vô lí vì tổng 4 góc trong một tứ giác bằng \(360^{\circ}\) ).
• Nếu tứ giác có 3 góc tù và 1 góc nhọn.
Tổng 3 góc tù lớn hơn: \(3.90^{\circ}=270^{\circ}\);
Số đo góc còn lại của tứ giác nhỏ hơn: \(360^{\circ}-270^{\circ}=90^{\circ}\) (thỏa mãn).
Do đó, một tứ giác có thể có nhiều nhất 3 góc tù.
Vậy một tứ giác có thể có nhiều nhất 3 góc nhọn; một tứ giác có thể có nhiều nhất 3 góc tù.

• Hình 3.8 a)

Xét tứ giác \(A B C D\) có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{\circ}\)
Hay \(90^{\circ}+90^{\circ}+{ }^{\wedge} \mathrm{C}+90^{\circ}=360^{\circ}\)
Khi đó \(\widehat{C}+270^{\circ}=360^{\circ}\)
Do đó \(\widehat{C}=360^{\circ}-270^{\circ}=90^{\circ}\).
Vậy \(\widehat{C}=90^{\circ}\)

• Hình 3.8 b)
 

Vì \(\widehat{\mathrm{VUS}}\) và \(\widehat{V U x}\) là hai góc kề bù nên ta có: \(\widehat{\mathrm{VUS}}+\widehat{V U x}=180^{\circ}\) Hay \(\widehat{\mathrm{VUS}}+60^{\circ}=180^{\circ}\)
Suy ra \(\widehat{\mathrm{VUS}}=180^{\circ}-60^{\circ}=120^{\circ}\)
Vì \(\widehat{U S R}\) và \(\widehat{U S y}\) là hai góc kề bù nên ta có: \(\widehat{U S R}+\widehat{U S y}=180^{\circ}\)
Hay \(\widehat{U S R}+110^{\circ}=180^{\circ}\)
Suy ra \(\widehat{U S R}=180^{\circ}-110^{\circ}=70^{\circ}\)
Do đó \(\widehat{U S R}=70^{\circ}\)
Xét tứ giác VUSR có:
\(\widehat{V}+\widehat{\mathrm{VUS}}+\widehat{V S R}+\widehat{R}=360^{\circ}\)
Hay \(90^{\circ}+120^{\circ}+70^{\circ}+\widehat{R}=360^{\circ}\)
Khi đó \(280^{\circ}+\widehat{R}=360^{\circ}\)
Do đó \(\widehat{\boldsymbol{R}}=360^{\circ}-280^{\circ}=80^{\circ}\)
Vậy \(\widehat{R}=80^{\circ}\)

Áp dụng định lí tổng bốn góc trong một tứ giác vào tứ giác HEFG, ta có:
\(\begin{aligned}& \widehat{H}+\widehat{E}+\widehat{F}+\widehat{G}=360^{\circ} \\& \widehat{E}+10^{\circ}+\widehat{E}+60^{\circ}+50^{\circ}=360^{\circ} \\& 2 \widehat{E}+120^{\circ}=360^{\circ}\end{aligned}\)
Suy ra \(2 \widehat{E}=360^{\circ}-120^{\circ}=240^{\circ}\)
Khi đó \(\widehat{E}=120^{\circ}\)
Suy ra \(\widehat{H}=\widehat{E}+10^{\circ}=120^{\circ}+10^{\circ}=130^{\circ}\)
Vậy \(\widehat{H}=130^{\circ} ; \widehat{E}=120^{\circ}\)

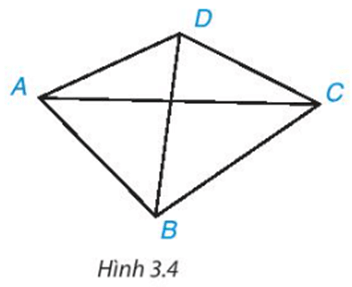
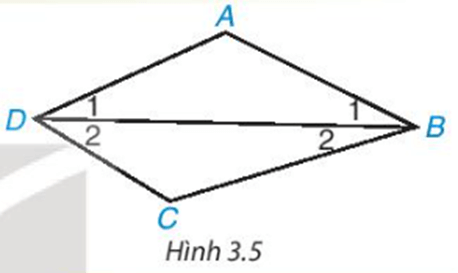
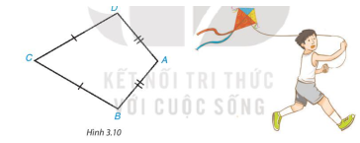
a) Nối \(A C, B D\) (như hình vẽ
Ta có \(A B=A D\) hay hai điểm \(A\) cách đều hai đầu mút \(B\) và \(D\); \(C B=C D\) hay hai điểm \(C\) cách đều hai đầu mút \(B\) và \(D\);
Do đó, hai điểm \(A\) và \(C\) cách đều hai đầu mút \(B\) và \(D\).
Vậy AC là đường trung trực của đoạn thẳng BD.

b) Gọi I là giao điểm của \(A C\) và \(B D\).
Vì \(\mathrm{AC}\) là đường trung trực của đoạn thẳng \(\mathrm{BD}\) nên \(\mathrm{AC} \perp \mathrm{BD}\).
- Xét tam giác \(A B D\) cân tại \(A(v i ̀ ~ A B=A D)\) có \(A\) l là đường cao (vì \(\mathrm{Al} \perp \mathrm{BD})\)
Nên Al cũng là tia phân giác của \(\widehat{B A D}\) hay \(\widehat{A_1}=\widehat{A_2}\)
Suy ra \(\widehat{A_1}=\widehat{A_2}=\widehat{B \mathrm{DA}}: 2=100^{\circ}: 2=50^{\circ}\)
- Xét tam giác \(\mathrm{BCD}\) cân tại \(\mathrm{C}\) (vì \(\mathrm{BC}=\mathrm{CD}\) ) có \(\mathrm{Cl}\) là đường cao (vì \(\mathrm{AC} \perp \mathrm{BD})\)
Nên CI cũng là tia phân giác của \(\widehat{B C D}\) hay \(\widehat{C_1}=\widehat{C_2}\)
Suy ra \(\widehat{C_1}=\widehat{C_2}=\widehat{B C D}: 2=60^{\circ}: 2=30^{\circ}\)
- Xét tam giác \(\mathrm{ACD}\) có: \(\widehat{A_1}+\widehat{C_1}+\widehat{A D C}=180^{\circ}\) (định lí tổng ba góc trong một tam giác).
Hay \(50^{\circ}+30^{\circ}+\widehat{A D C}=180^{\circ}\)
Suy ra \(\widehat{A D C}=180^{\circ}-50^{\circ}-30^{\circ}=100^{\circ}\)
Xét tứ giác \(A B C D\) có:
\(\widehat{B A \mathrm{D}}+\widehat{A B C}+\widehat{B C \mathrm{D}}+\widehat{A D C}=360^{\circ}\) (định lí tổng bốn góc của một tứ giác).
Hay \(100^{\circ}+\widehat{A B C}+60^{\circ}+100^{\circ}=360^{\circ}\)
Suy ra \(\widehat{A B C}+260^{\circ}=360^{\circ}\)
Do đó \(\widehat{A B C}=360^{\circ}-260^{\circ}=100^{\circ}\)
Vậy \(\widehat{A B C}=100^{\circ} ; \widehat{A D C}=100^{\circ}\)