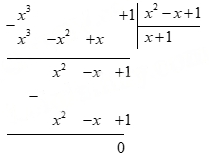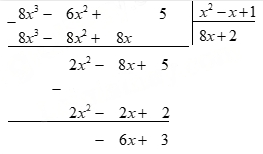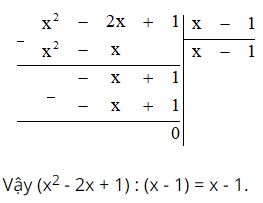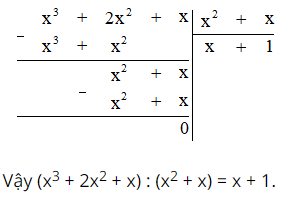Khởi động
64
Trong quá trình biến đổi và tính toán những biểu thức đại số, nhiều khi ta phải thực hiện phép chia một đa thức (một biến) cho một đa thức (một biến) khác, chẳng hạn ta cần thực hiện phép chia sau:
\(({x^3} + 1):({x^2} - x + 1)\)
Làm thế nào để thực hiện được phép chia một đa thức cho một đa thức khác?
Gợi ý
Đọc kĩ phần III. Chia đa thức một biến đã sắp xếp.
Đáp án
Để thực hiện phép chia một đa thức cho một đa thức khác, ta làm như sau:
Bước 1:
- Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.
- Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.
- Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.
Bước 2: Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.