80
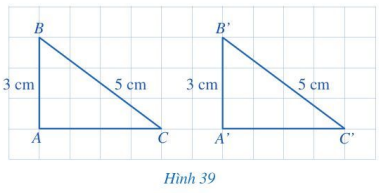
Giá để đồ ở Hình 33 gợi nên hình ảnh hai tam giác ABC và A’B’C’ có: AB = A’B’, BC = B’C’, CA = C’A’.
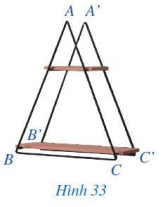
Tam giác ABC có bằng tam giác A’B’C’ hay không?
Quan sát Hình 33 để xem tam giác ABC có bằng tam giác A’B’C’ không.
Tam giác ABC có bằng tam giác A’B’C’ (vì 2 tam giác này có thể chồng khít lên nhau).
81
Hai tam giác ở Hình 37 có bằng không? Vì sao?
Hai tam giác bằng nhau nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia.
Xét tam giác ABC và tam giác ABD:
AC = AD; BC = BD, cạnh AB chung.
Vậy \(\Delta ABC = \Delta ABD\)(c.c.c)
82
Cho hai tam giác vuông ABC và A’B’C’ có: \(\widehat A = \widehat {A'} = 90^\circ ,AB = A'B' = 3\)cm,\(BC = B'C' = 5\)cm (Hình 39). So sánh độ dài các cạnh AC và A’C’.
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Xét tam giác ABC và tam giác A’B’C’:
AB = A’B’ = 3 cm; BC = B’C’ = 5 cm; AC = A’C’ = 4 cm.
Vậy tam giác ABC bằng tam giác A’B’C’. (c.c.c)
83
Cho Hình 42 có MN = QN, MP = QP. Chứng minh \(\widehat {MNP} = \widehat {QNP}\).
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Hai tam giác bằng nhau thì các cặp cạnh tương ứng và các cặp góc tương ứng bằng nhau.
Xét tam giác MNP và tam giác QNP: MN = QN; MP = QP; NP chung.
Vậy \(\Delta MNP = \Delta QNP\) (c.c.c)
Vậy \(\widehat {MNP} = \widehat {QNP}\) ( 2 góc tương ứng)
83
Cho Hình 43 có AB = AD, \(\widehat {ABC} = \widehat {ADC} = 90^\circ\). Chứng minh \(\widehat {ACB} = \widehat {ACD}\).
Nếu một cạnh góc vuông và một cạnh huyền của tam giác vuông này bằng một cạnh góc vuông và một cạnh huyền của tam giác kia thì hai tam giác vuông đó bằng nhau.
Hai tam giác bằng nhau thì các cặp góc tương ứng bằng nhau.
Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung.
Nên \(\Delta ABC = \Delta ADC\) (cạnh huyền - cạnh góc vuông) nên \(\widehat {ACB} = \widehat {ACD}\) (2 góc tương ứng)
83
Cho Hình 44 có AC = BD, \(\widehat {ABC} = \widehat {BAD} = 90^\circ\). Chứng minh AD = BC.
Nếu một cạnh góc vuông và một cạnh huyền của tam giác vuông này bằng một cạnh góc vuông và một cạnh huyền của tam giác kia thì hai tam giác vuông đó bằng nhau.
Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau.
Xét hai tam giác vuông DAB và CBA: AC = BD; AB chung.
Nên \(\Delta DAB = \Delta CBA\) (cạnh huyền - cạnh góc vuông)
Nên AD = BC ( 2 cạnh tương ứng)
83
Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP, \(\widehat A = 65^\circ ,\widehat N = 71^\circ \). Tính số đo các góc còn lại của hai tam giác.
Hai tam giác bằng nhau thì các cặp góc tương ứng bằng nhau. Và tổng ba góc trong một tam giác bằng 180°.
Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP, AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau: \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Vậy \(\widehat A = \widehat M = 65^\circ\); \(\widehat B = \widehat N = 71^\circ\); \(\widehat C = \widehat P = 180^\circ - 65^\circ - 71^\circ = 44^\circ\)(vì tổng ba góc trong một tam giác bằng 180°).
