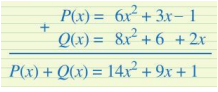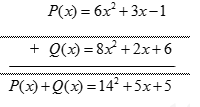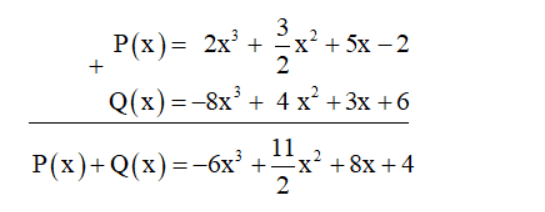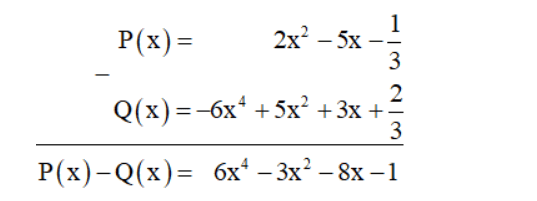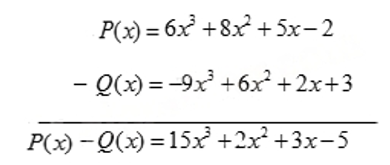Khởi động
54
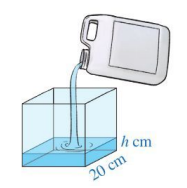
Một số tình huống trong cuộc sống dẫn đến việc cộng, trừ hai đa thức một biến, chẳng hạn, ta phải tính tổng diện tích các mặt của hình hộp chữ nhật (Hình 2) có độ dài hai cạnh đáy là x (m), 2x (m) và chiều cao là 2 (m).
Phép cộng, phép trừ hai đa thức một biến được thực hiện như thế nào?
Gợi ý
Đọc lại bài (Phần I để xem cách cộng hai đa thức và phần II để xem cách trừ hai đa thức).
Đáp án
a) Cộng hai đa thức:
Để cộng hai đa thức một biến (theo cột dọc), ta có thể làm như sau:
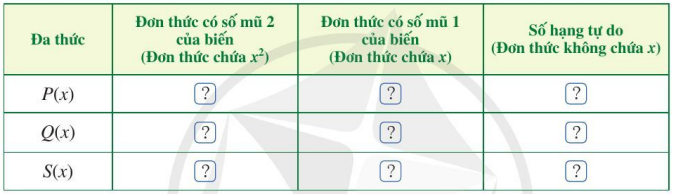
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột;
- Cộng hai đơn thức trong từng cột, ta có tổng cần tìm.
Để cộng hai đa thức một biến (theo hàng ngang), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết tổng hai đơn thức theo hàng ngang;
- Nhóm các đơn thức có cùng số mũ của biến với nhau;
- Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.
b) Trừ hai đa thức:
Để trừ đa thức P(x) cho đa thức Q(x) (theo cột dọc), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức P(x) ở trên và đơn thức của Q(x) ở dưới;
- Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
Để trừ đa thức P(x) cho đa thức Q(x) (theo hàng ngang), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc;
- Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau;
- Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.