Bài 3: Hai tam giác bằng nhau

Khởi động

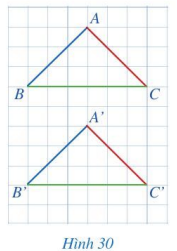
Một dây chuyền sản xuất ra các sản phẩm có dạng hình tam giác giống hệt nhau (Hình 27). Khi đóng gói hàng, người ta xếp chúng chồng khít lên nhau.

Khi hai tam giác có thể chồng khít lên nhau thì các cạnh và các góc tương ứng liên hệ với nhau như thế nào?

Gợi ý

Học sinh có thể cụ thể hóa dây chuyền sản xuất đó bằng cách cắt các hình tam giác giống nhau rồi chồng chúng lên nhau.

Đáp án

Khi hai tam giác có thể trồng khít lên nhau thì các cạnh tương ứng của hai tam giác bằng nhau và các góc tương ứng của hai tam giác bằng nhau.

Hoạt động 2

Quan sát hai tam giác ABC và A’B’C’ trên một tờ giấy kẻ ô vuông (Hình 30).

a) So sánh:

- Các cặp cạnh: AB và A’B’; BC và B’C’; CA và C’A’.

- Các cặp góc: A và A’; B và B’; C và C’.

b) Hai tam giác ABC và A’B’C’ có bằng nhau hay không?

c) Cắt mảnh giấy hình tam giác ABC và mảnh giấy hình tam giác A’B’C’, hai hình tam giác đó có thể đặt chồng khít lên nhau hay không?

Gợi ý

a) Học sinh quan sát Hình 30 để so sánh các cặp cạnh và cặp góc.

b) Hai tam giác ABC và A’B’C’ có bằng nhau hay không thì ta dựa vào mối liên hệ giữa các cặp cạnh và các cặp góc tương ứng của hai tam giác.

c) Học sinh tự thực hành cắt mảnh giấy để đưa ra kết luận.

Đáp án

a) AB = A’B’; BC = B’C’; CA = C’A’.

\(\widehat{A} = \widehat{A'} ; \widehat{B} = \widehat{B'} ; \widehat{C} = \widehat{C'} \)

b) Hai tam giác ABC và A’B’C’ có bằng nhau vì chúng có các cặp cạnh và cặp góc tương ứng bằng nhau.

c) Hai hình tam giác ABC và A’B’C’ có thể đặt chồng khít lên nhau.

Luyện tập vận dụng

Cho biết \(\Delta ABC = \Delta MNP\), \(AC = 4\)cm, \(\widehat {MPN} = 45^\circ \). Tính độ dài cạnh MP và số đo góc ACB.

Gợi ý

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng và các góc tương ứng bằng nhau.

Đáp án

\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).

Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ\).

Bài tập 1

Cho biết \(\Delta ABC = \Delta DEG\),\(AB = 3\)cm,\(BC = 4\)cm,\(CA = 6\)cm. Tìm độ dài các cạnh của tam giác DEG.

Gợi ý

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng và các góc tương ứng bằng nhau.

Đáp án

\(\Delta ABC = \Delta DEG\) nên AB = DE, BC = EG, CA = GD.

Vậy độ dài các cạnh của tam giác DEG lần lượt là: \(DE = 3\)cm,\(EG = 4\)cm,\(GD = 6\)cm.

Bài tập 2

Cho biết \(\Delta PQR = \Delta IHK\),\(\widehat P = 71^\circ ,\widehat Q = 49^\circ \). Tính số đo góc K của tam giác IHK.

Gợi ý

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng và các góc tương ứng bằng nhau.

Tổng ba góc trong một tam giác bằng 180°.

Đáp án

Ta có: \(\Delta PQR = \Delta IHK\)nên \(\widehat P = \widehat I;\widehat Q = \widehat H;\widehat R = \widehat K\).

\(\Rightarrow \widehat I = 71^\circ ,\widehat H = 49^\circ\). Mà tổng 3 góc trong một tam giác bằng 180° nên trong tam giác IHK:

\(\widehat I + \widehat H + \widehat K = 180^\circ\)

Vậy \(\widehat K = 180^\circ - 71^\circ - 49^\circ = 60^\circ\).

Bài tập 3

Cho \(\Delta ABC = \Delta MNP\) và \(\widehat A + \widehat N = 125^\circ \). Tính số đo góc P.

Gợi ý

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng và các góc tương ứng bằng nhau.

Tổng ba góc trong một tam giác bằng 180°.

Đáp án

Ta có: \(\Delta ABC = \Delta MNP\) nên \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).

Mà \(\widehat A + \widehat N = 125^\circ\)hay \(\widehat M + \widehat N = 125^\circ\). Tổng ba góc trong một tam giác bằng 180°.

Trong tam giác MNP:

\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\125^\circ+ \widehat P = 180^\circ \\ \to \widehat P = 180^\circ- 125^\circ= 55^\circ \end{array}\)

Vậy số đo góc P là 55°.

Bài tập 4

Cho tam giác ABC và điểm M thuộc cạnh BC thỏa mãn \(\Delta AMB = \Delta AMC\)(Hình 32). Chứng minh rằng:

a) M là trung điểm của đoạn thẳng BC.

b) Tia AM là tia phân giác của góc BAC và \(AM \bot BC\).

Gợi ý

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng và các góc tương ứng bằng nhau.

a) Muốn chứng minh M là trung điểm của đoạn thẳng BC, ta chứng minh MB = MC.

b) Muốn chứng minh tia AM là phân giác của góc BAC ta chứng minh góc BAM = góc CAM.

Trong một tam giác, một đường thẳng vừa là trung tuyến vừa là phân giác thì đường thẳng đó vuông góc với đáy tương ứng. Hoặc ta có thể chứng minh góc được tạo bởi hai đường thẳng đó có số đo góc là 90°.

Đáp án

a) Ta có:\(\Delta AMB = \Delta AMC\)nên AB = AC, MB = MC nên M là trung điểm của đoạn thẳng BC.

b) Ta có:\(\Delta AMB = \Delta AMC\)nên \(\widehat {AMB} = \widehat {AMC},\widehat {MAB} = \widehat {MAC},\widehat {MBA} = \widehat {MCA}\).

Vậy tia AM là tia phân giác của góc BAC vì \(\widehat {MAB} = \widehat {MAC}\).

Ta thấy:\(\widehat {AMB} = \widehat {AMC}\)mà ba điểm B, M, C thẳng hàng nên \(\widehat {BMC} = 180^\circ\).

\(\Rightarrow \widehat {AMB} = \widehat {AMC} = \dfrac{1}{2}.\widehat {BMC} = \dfrac{1}{2}.180^\circ = 90^\circ\). Vậy \(AM \bot BC\).