Bài 3: Hai đường thẳng song song

Theo em dự đoán, hai góc đó có bằng nhau

Hình 38a: a và b song song

Hình 38b: không có 2 đường thẳng nào song song

Hình 38c: m và n song song

b) Đường thẳng b song song với đường thẳng a vì đường thẳng c cắt 2 đường thẳng a và b tạo ra một cặp góc đồng vị bằng nhau

Vì u // v nên x = 50\(^\circ \) ( 2 góc so le trong)

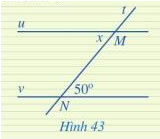
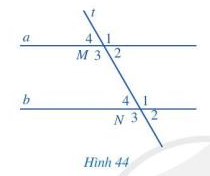
a) Vì a // b nên \(\widehat {{M_1}} = \widehat {{N_1}}\); \(\widehat {{M_4}} = \widehat {{N_4}}\) ( 2 góc đồng vị) mà \(\widehat {{N_3}} = \widehat {{N_1}}\) ; \(\widehat {{N_4}} = \widehat {{N_2}}\) ( 2 góc đối đỉnh) nên \(\widehat {{M_1}}\) =\(\widehat {{N_3}}\); \(\widehat {{M_4}}\) =\(\widehat {{N_2}}\)

b) Vì a // b nên \(\widehat {{M_2}} = \widehat {{N_2}};\widehat {{M_3}} = \widehat {{N_3}}\) ( 2 góc đồng vị), mà \(\widehat {{N_1}} + \widehat {{N_2}} = 180^\circ ;\widehat {{N_3}} + \widehat {{N_4}} = 180^\circ\) ( 2 góc kề bù) nên \(\widehat {{M_2}} + \widehat {{N_1}}\) = 180\(^\circ\); \(\widehat {{M_3}} + \widehat {{N_4}}\)= 180\(^\circ\)

Chú ý:

Nếu đường thẳng c  cắt cả hai đường thẳng song song a và b thì:

+ Hai góc so le ngoài bằng nhau

+ Hai góc trong cùng phía có tổng số đo bằng 180\(^\circ\)

a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ\) ( 2 góc kề bù) nên \(117^\circ  + \widehat {{A_2}} = 180^\circ  \Rightarrow \widehat {{A_2}} = 180^\circ  - 117^\circ  = 63^\circ\)

Vì \(\widehat {{A_2}} = \widehat {{D_1}}\) ( cùng bằng 63 độ)

Mà 2 góc này ở vị trí đồng vị

\(\Rightarrow\) a // b (Dấu hiệu nhận biết hai đường thẳng song song) ( đpcm)

b) Vì a // b nên \(\widehat {{B_1}} = \widehat {BCD}\) ( 2 góc so le trong), mà \(\widehat {{B_1}} = 55^\circ  \Rightarrow \widehat {BCD} = 55^\circ\)

Ta có: \(\widehat{xOa}+\widehat{aOy}=\widehat{xOy} \Rightarrow \widehat{aOy}=144^0-90^0=54^0\) 

Vì AB // Oy nên \(\widehat {aOy} = \widehat {{A_2}}\) ( 2 góc đồng vị) \(\Rightarrow \widehat {{A_2}} = 54^\circ\)

Vì a // b nên \(\widehat {{B_1}} = \widehat {{A_2}}\) ( 2 góc đồng vị) \(\Rightarrow \widehat {{B_1}} = 54^\circ\)