Khởi động
44
Hình 5 mô tả một vật chuyển động từ điểm gốc O theo chiều ngược với chiều dương của trục số. Sau 1 giờ, vật đến điểm -40 trên trục số (đơn vị đo trên trục số là ki-lô-mét)
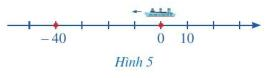
Hỏi vật đã chuyển động được quãng đường bao nhiêu ki-lô-mét sau 1 giờ?
Làm thế nào để biểu diễn được quãng đường đó thông qua số thực -40?
Gợi ý
Khoảng cách từ 0 đến -40 là quãng đường vật đã chuyển động được trong 1 giờ.
Đáp án
Vật đã chuyển động được quãng đường là:
0 – (- 40) = 40 (km)
Để biểu diễn được quãng đường đó thông qua số thực -40, ta sử dụng khái niệm giá trị tuyệt đối (|-40|=40)