81
Trong thực tiễn ta thường gặp những đồ vật có hình khối như ở Hình 18 và Hình 19.
Những hình khối có dạng như trên được gọi là hình gì?
Dựa vào hiểu biết thực tiễn
Những hình khối như trên được gọi là hình lăng trụ.
82
Quan sát lăng trụ đứng tam giác ở Hình 22, đọc tên các mặt, các cạnh và các đỉnh của lăng trụ đứng tam giác đó.
Đọc tên 5 mặt, 9 cạnh, 6 đỉnh của hình lăng trụ đứng tam giác
Hình lăng trụ đứng tam giác có:
+) 5 mặt gồm: ABC; A’B’C’; ABB’A’; BCC’B’; ACC’A’
+) 9 cạnh gồm: AB; BC;CA;A’B’;B’C’;C’A’; AA’; BB’; CC’
+) 6 đỉnh gồm: A;B;C; A’;B’;C’.
82
Quan sát hình lăng trụ đứng tam giác ABC.A’B’C’ ở Hình 23 và thực hiện các hoạt động sau:
a) Đáy dưới ABC và đáy trên A’B’C’ là hình gì?
b) Mặt bên AA’C’C là hình gì?
c) So sánh độ dài các cạnh bên AA’ và CC’
Hình lăng trụ đứng tam giác có 2 mặt đáy là hình tam giác, mặt bên là các hình chữ nhật
So sánh độ dài 2 cạnh
a) Đáy dưới ABC và đáy trên A’B’C’ là hình tam giác
b) Mặt bên AA’C’C là hình chữ nhật
c) Hai cạnh bên AA’ và CC’ có độ dài bằng nhau
83
Quan sát hình lăng trụ đứng tứ giác ở Hình 26, đọc tên các mặt, các cạnh, các đỉnh và các đường chéo của hình lăng trụ đứng tứ giác đó.
Đọc tên 6 mặt, 12 cạnh, 8 đỉnh của hình lăng trụ đứng tứ giác
Hình lăng trụ đứng tứ giác ABCD. A’B’C’D’ có:
+) 6 mặt gồm: ABCD; A’B’C’D’; ABB’A’; ADD’A’; BCC’B’; CDD’C’.
+) 12 cạnh gồm: AB; BC;CD;DA;A’B’;B’C’;C’D’; D’A’; AA’; BB’; CC’ ; DD’.
+) 8 đỉnh gồm: A;B;C;D;A’;B’;C’;D’.
83
Quan sát hình lập phương ABCD. A’B’C’D’ ở Hình 27 và cho biết:
a) Đáy dưới ABCD và đáy trên A’B’C’D’ là hình gì?
b) Mặt bên AA’D’D là hình gì?
c) So sánh độ dài hai cạnh bên AA’ và DD’.
Hình lăng trụ đứng tứ giác có 2 mặt đáy là hình tứ giác, mặt bên là hình chữ nhật
Các cạnh bên bằng nhau
a) Đáy dưới ABCD và đáy trên A’B’C’D’ là hình tứ giác
b) Mặt bên AA’D’D là hình chữ nhật
c) Độ dài hai cạnh bên AA’ và DD’ bằng nhau.
84
Nêu công thức tính thể tích hình hộp chữ nhật ABCD.A’B’C’D’.
Công thức tính thể tích hình hộp chữ nhật
Công thức tính thể tích hình hộp chữ nhật là: S.h với S là diện tích đáy; h là chiều cao của hình hộp
84
Quan sát hình lăng trụ đứng tam giác (Hình 30). Trải mặt bên AA’C’C thành hình chữ nhật AA’MN. Trải mặt bên BB’C’C thành hình chữ nhật BB’QP.
a) Tính diện tích hình chữ nhật MNPQ
b) So sánh diện tích của hình chữ nhật MNPQ với tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó.
c) So sánh diện tích của hình chữ nhật MNPQ với diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’
Diện tích hình chữ nhật = chiều dài . chiều rộng
Tính và so sánh
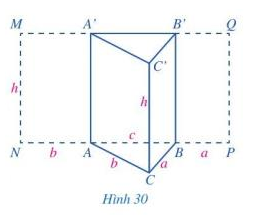
a) Diện tích hình chữ nhật MNPQ là: \(S = MN . NP = h.(b+c+a)\)
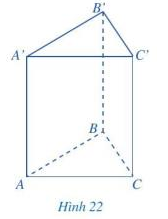
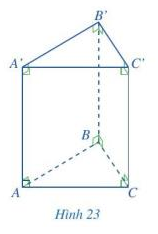
b) Chu vi đáy của hình lăng trụ tam giác là: \(C_{ABC}\) = a+b+c
Tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó là:
\((a+b+c).h\)
Như vậy, diện tích của hình chữ nhật MNPQ bằng tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó
c) Diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’ là:
\(S_{xq}\) = \(S_{ABB’A’ }\)+ \(S_{ACC’A’}\) + \(S_{BCC’B’}\) = \(h.c+h.b+h.a \) = \(h.(c+b+a)\)
Vậy diện tích của hình chữ nhật MNPQ bằng diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’
85
Tìm số thích hợp cho ? trong bảng sau:
Đặc điểm của hình lăng trụ đứng tam giác và lăng trụ đứng tứ giác
86
Chọn từ đúng (Đ), sai (S) thích hợp cho ? trong bảng sau:
Đặc điểm của hình lăng trụ đứng tam giác và lăng trụ đứng tứ giác
Diện tích xung quanh, thể tích của hình lăng trụ đứng tam giác và lăng trụ đứng tứ giác
86
Cho các hình 33a và hình 33b:
i) Hình nào trong các hình 33a, 33b là hình lăng trụ đứng tam giác? Hình lăng trụ đứng tứ giác?
ii) Tính diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác có ở Hình 33.
iii) Tính thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác có ở Hình 33.
+) Hình lăng trụ đứng tam giác có 2 mặt đáy cùng là hình tam giác và song song với nhau; mỗi mặt bên là hình chữ nhật.
+) Hình lăng trụ đứng tứ giác có 2 mặt đáy cùng là hình tứ giác và song song với nhau; mỗi mặt bên là hình chữ nhật.
+) Diện tích xung quanh của hình lăng trụ đứng = chu vi đáy . chiều cao
+) Thể tích của hình lăng trụ đứng = diện tích đáy . chiều cao
i) Hình 33b là hình lăng trụ đứng tam giác
Hình 33a là hình lăng trụ đứng tứ giác
ii) Hình 33a: Sxq = (3+4+5+8).5 = 100 (\(cm^2\))
Hình 33b: Sxq = (3+4+5).6 = 72 (\(cm^2\))
iii) Hình 33a: Diện tích đáy là: (8+4).3:2=18 (\(cm^2\))
Thể tích là: V = 18.5 = 90 (\(cm^3\))
Hình 33b: Diện tích đáy là: \(\dfrac{1}{2}3.4=6\) (\(cm^2\))
Thể tích là: V= 6.6=36 (\(cm^3\))
