47
Trong giờ học môn Mĩ thuật, bạn Hạnh dán lên Trvở hai hình vuông có kích thước lần lượt là 3 cm và x cm như ở Hình 1. Tổng diện tích của hai hình vuông đó là \({x^2} + 9(c{m^2})\).
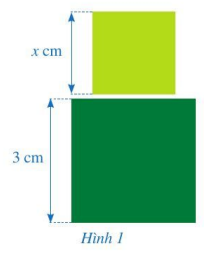
Biểu thức đại số \({x^2} + 9\)có gì đặc biệt?
Quan sát biểu thức và đưa ra sự đặc biệt của biểu thức so với những biểu thức tính diện tích trước đó.
Biểu thức đại số \({x^2} + 9\) xuất hiện biến x trong phép tính tính tổng diện tích của hai hình vuông.
47
a) Viết biểu thức biểu thị:
- Diện tích hình vuông có độ dài cạnh là x cm;
- Thể tích của hình lập phương có độ dài cạnh là 2x cm.
b) Các biểu thức trên có dạng như thế nào?
a) Diện tích hình vuông bằng cạnh nhân cạnh.
Thể tích của hình lập phương bằng cạnh mũ 3.
b) Quan sát hai kết quả của phần a để đưa ra kết luận.
a) Biểu thức biểu thị:
- Diện tích hình vuông có độ dài cạnh là x cm là \(x.x = {x^2}(c{m^2})\)
- Thể tích của hình lập phương có độ dài cạnh là 2x cm là \({(2x)^3} = 8{x^3}(c{m^3})\)
b) Các biểu thức trên có dạng một biến với lũy thừa có số mũ nguyên dương của biến đó.
47
a) Viết biểu thức biểu thị:
- Quãng đường ô tô đi được trong thời gian x (h), nếu vận tốc là 60 km/h;
- Tổng diện tích của các hình: hình vuông có độ dài cạnh là 2x cm; hình chữ nhật có các kích thước là 3 cm và x cm; hình thoi có độ dài hai đường chéo là 4 cm và 8 cm.
b) Các biểu thức trên có bao nhiêu biến? Mỗi số hạng xuất hiện trong biểu thức có dạng như thế nào?
a) Quãng đường đi được bằng vận tốc nhân thời gian.
Tổng diện tích các hình bằng diện tích của từng hình cộng lại. (diện tích hình vuông bằng cạnh nhân cạnh; diện tích hình chữ nhật bằng chiều dài nhân chiều rộng, diện tích hình thoi bằng một nửa tích độ dài hai đường chéo).
b) Quan sát vào biểu thức của phần a để đưa ra biểu thức có bao nhiêu biến và mỗi số hạng xuất hiện có dạng như thế nào?
a) Biểu thức biểu thị:
- Quãng đường ô tô đi được trong thời gian x (h), nếu vận tốc là 60 km/h là \(60x\) (km).
- Tổng diện tích của các hình: hình vuông có độ dài cạnh là 2x cm; hình chữ nhật có các kích thước là 3 cm và x cm; hình thoi có độ dài hai đường chéo là 4 cm và 8 cm là
\({(2x)^2} + 3.x + \dfrac{1}{2}.4.8 = 4{x^2} + 3x + 16\)
b) Các biểu thức trên có 1 biến (biến x). Mỗi số hạng xuất hiện trong biểu thức (60x, \(4x^2\), 3x) đều là tích của một số nhân một biến và số hạng (8) là dạng số hoặc đơn thức với số mũ của x bằng 0.
48
Biểu thức nào sau đây là đa thức một biến?
a) \({x^2} + 9;\)
b) \(\dfrac{2}{{{x^2}}} + 2x + 1;\)
c) \(3x + \dfrac{2}{5}y.\)
Đa thức một biến là tổng những đơn thức của cùng một biến. Mỗi đơn thức cũng là một đa thức
a) \({x^2} + 9\) là đa thức một biến x.
b) \(\dfrac{2}{{{x^2}}} + 2x + 1\) không phải là đa thức một biến x.
c) \(3x + \dfrac{2}{5}y\) không phải là đa thức một biến x hay y.
48
Cho hai đơn thức của cùng biến x là \(2{x^2}\)và \(3{x^2}\).
a) So sánh số mũ của biến x trong hai đơn thức trên.
b) Thực hiện phép cộng \(2{x^2} + 3{x^2}\).
c) So sánh kết quả của hai phép tính: \(2{x^2} + 3{x^2}\) và \((2 + 3){x^2}\).
a) Dựa vào số mũ của x trong hai đơn thức để so sánh.
b) Thực hiện phép cộng như bình thường. (Tách các số để cộng).
c) Thực hiện phép tính \((2 + 3){x^2}\) để so sánh kết quả của hai phép tính.
a) Ta thấy: số mũ của x trong hai đơn thức trên bằng nhau (đều bằng 2).
b) \(2{x^2} + 3{x^2} = {x^2} + {x^2} + {x^2} + {x^2} + {x^2} = 5{x^2}\) .
c) Ta có: \((2 + 3){x^2} = 5{x^2}\).
Vậy \(2{x^2} + 3{x^2}\) = \((2 + 3){x^2}\).
49
Thực hiện mỗi phép tính sau:
a) \({x^2} + \dfrac{1}{4}{x^2} - 5{x^2}\);
b) \({y^4} + 6{y^4} - \dfrac{2}{5}{y^4}\).
Để cộng (hay trừ) hai đơn thức có cùng số mũ của biến, ta cộng (hay trừ) hai hệ số với nhau và giữ nguyên phần biến.
a) x là biến.
b) y là biến.
a) \({x^2} + \dfrac{1}{4}{x^2} - 5{x^2} = (1 + \dfrac{1}{4} - 5){x^2} = - \dfrac{{15}}{4}{x^2}\);
b) \({y^4} + 6{y^4} - \dfrac{2}{5}{y^4} = (1 + 6 - \dfrac{2}{5}){y^4} = \dfrac{{33}}{5}{y^4}\).
49
Cho đa thức \(P(x) = {x^2} + 2{x^2} + 6x + 2x - 3\).
a) Nêu các đơn thức của biến x có trong đa thức P(x).
b) Tìm số mũ của biến x trong từng đơn thức nói trên.
c) Thực hiện phép cộng các đơn thức có cùng số mũ của biến x sao cho trong đơn thức P(x) không còn hai đơn thức nào có cùng số mũ của biến x.
a) Mỗi đơn thức (một biến x) nếu không phải là một số thì có dạng \(a{x^k}\), trong đó a là số thực khác 0 và k là số nguyên dương.
b) Một số thực khác 0 cũng được coi là đơn thức với số mũ của biến bằng 0.
c) Nhóm những đơn thức có cùng số mũ của biến rồi thực hiện phép tính như bình thường
a) Các đơn thức của biến x có trong đa thức P(x) là: \({x^2},2{x^2},6x,2x,( - 3)\).
b) Số mũ của biến x trong các đơn thức \({x^2},2{x^2},6x,2x,( - 3)\) lần lượt là: 2; 2; 1; 1; 0.
c) \(P(x) = {x^2} + 2{x^2} + 6x + 2x - 3 = ({x^2} + 2{x^2}) + (6x + 2x) - 3 = 3{x^3} + 8x - 3\)
49
Thu gọn đa thức
\(P(y) = - 2{y^3} + y + \dfrac{{11}}{7}{y^3} + 3{y^2} - 5 - 6{y^2} + 9\).
Ta thực hiện phép cộng các đơn thức có cùng số mũ của biến y sao cho trong đa thức P(y) không còn hai đơn thức nào có cùng số mũ của biến y.
\(\begin{array}{l}P(y) =- 2{y^3} + y + \dfrac{{11}}{7}{y^3} + 3{y^2} - 5 - 6{y^2} + 9 = ( - 2{y^3} + \dfrac{{11}}{7}{y^3}) + (3{y^2} - 6{y^2}) + y + ( - 5 + 9)\\ =- \dfrac{3}{7}{y^3} - 3{y^2} + y + 4\end{array}\)
49
Cho đa thức \(R(x) = - 2{x^2} + 3{x^2} + 6x + 8{x^4} - 1\).
a) Thu gọn đa thức R(x).
b) Trong dạng thu gọn của đa thức R(x), sắp xếp các đơn thức theo số mũ giảm dần của biến.
a) Ta thực hiện phép cộng các đơn thức có cùng số mũ của biến x sao cho trong đa thức R(x) không còn hai đơn thức nào có cùng số mũ của biến x.
b) So sánh số mũ của biến trong các đơn thức để sắp xếp.
a) \(R(x) = - 2{x^2} + 3{x^2} + 6x + 8{x^4} - 1 = ( - 2{x^2} + 3{x^2}) + 6x + 8{x^4} - 1 = {x^2} + 6x + 8{x^4} - 1\)
b) Trong các đơn thức của đa thức R(x) ta thấy, số mũ lớn nhất là 4, sau đó đến 2; 1 và 0.
Vậy \(R(x) = {x^2} + 6x + 8{x^4} - 1 = 8{x^4} + {x^2} + 6x - 1\).
50
Sắp xếp đa thức
\(H(x) = - 0,5{x^8} + 4{x^3} + 5{x^{10}} - 1\) theo:
a) Số mũ giảm dần của biến;
b) Số mũ tăng dần của biến.
Sắp xếp đa thức (một biến) theo số mũ giảm dần (hoặc tăng dần) của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần (hoặc tăng dần) của biến.
Trong đa thức H(x), số mũ của đơn thức giảm dần là: 10; 8; 3; 0.
a) \(H(x) = - 0,5{x^8} + 4{x^3} + 5{x^{10}} - 1 = 5{x^{10}} - 0,5{x^8} + 4{x^3} - 1\).
b) \(H(x) = - 0,5{x^8} + 4{x^3} + 5{x^{10}} - 1 = - 1 + 4{x^3} - 0,5{x^8} + 5{x^{10}}\)
50
Cho đa thức \(P(x) = 9{x^4} + 8{x^3} - 6{x^2} + x - 1 - 9{x^4}\).
a) Thu gọn đa thức P(x).
b) Tìm số mũ cao nhất của x trong dạng thu gọn của P(x).
a) Ta thực hiện phép cộng các đơn thức có cùng số mũ của biến x sao cho trong đa thức P(x) không còn hai đơn thức nào có cùng số mũ của biến x.
b) So sánh số mũ của x trong các đơn thức của P(x) để đưa ra số mũ cao nhất.
a) \(P(x) = 9{x^4} + 8{x^3} - 6{x^2} + x - 1 - 9{x^4} = (9{x^4} - 9{x^4}) + 8{x^3} - 6{x^2} + x - 1 = 8{x^3} - 6{x^2} + x - 1\)
b) Số mũ cao nhất của x trong dạng thu gọn của P(x) là 3.
51
Cho đa thức
\(R(x) = - 1975{x^3} + 1945{x^4} + 2021{x^5} - 4,5\).
a) Sắp xếp đa thức R(x) theo số mũ giảm dần của biến.
b) Tìm bậc của đa thức R(x).
c) Tìm hệ số cao nhất và hệ số tự do của đa thức R(x).
a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến.
b) Bậc của đa thức là số mũ cao nhất của đa thức.
c) Hệ số cao nhất của đa thức là số đi cùng với biến có số mũ cao nhất. Hệ số tự do là số không đi cùng với biến (hay mũ của biến bằng 0).
a) \(R(x) = - 1975{x^3} + 1945{x^4} + 2021{x^5} - 4,5 = 2021{x^5} + 1945{x^4} - 1975{x^3} - 4,5\)
b) Bậc của đa thức R(x) là bậc 5 vì số mũ cao nhất của x trong đa thức là 5.
c) Đa thức R(x) có hệ số cao nhất là 2021 và hệ số tự do là – 4,5.
51
a) Tính giá trị của biểu thức đại số \(3x - 2\) tại x = 2.
b) Tính giá trị của đa thức P(x) = \(- 4x + 6\) tại x = – 3.
Thay các giá trị của x vào biểu thức, đa thức rồi thực hiện phép tính.
a) Tại x = 2, giá trị của biểu thức đại số \(3x - 2\)= \(3.2 - 2 = 6 - 2 = 4\).
b) Tại x = – 3, giá trị của đa thức P(x) = \(- 4x + 6\) bằng:
\(P( - 3) = - 4. - 3 + 6 = 12 + 6 = 18\).
51
Cho đa thức \(P(x) = {x^2} - 3x + 2\). Tính P(1), P(2).
Thay các giá trị của x vào đa thức rồi thực hiện phép tính.
\(P(1) = {1^2} - 3.1 + 2 = 1 - 3 + 2 = 0\).
\(P(2) = {2^2} - 3.2 + 2 = 4 - 6 + 2 = 0\).
52
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) x = 4 và x = – 4 là nghiệm của đa thức\(P(x) = {x^2} - 16\).
b) y = – 2 là nghiệm của đa thức \(Q(y) = - 2{y^3} + 4\).
Muốn kiểm tra phát biểu nào đúng, phát biểu nào sai; ta thay các giá trị x, y vào 2 đa thức đã cho để kiểm tra.
Một giá trị là nghiệm của đa thức khi và chỉ khi giá trị đó khi thay vào đa thức làm cho giá trị của đa thức bằng 0.
a) \(P(4) = {4^2} - 16 = 16 - 16 = 0\).
\(P( - 4) = {( - 4)^2} - 16 = 16 - 16 = 0\).
Vậy x = 4 và x = – 4 là nghiệm của đa thức \(P(x) = {x^2} - 16\). Phát biểu a) đúng.
b) \(Q( - 2) = - 2.{( - 2)^3} + 4 = - 2. (- 8) + 4 = 16 + 4 = 20 \ne 0\).
Vậy y = – 2 không là nghiệm của đa thức \(Q(y) = - 2{y^3} + 4\). Phát biểu b) sai.
52
Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.
a) \(- 2x\)
b) \(- {x^2} - x + \dfrac{1}{2}\) ;
c) \(\dfrac{4}{{{x^2} + 1}} + {x^2}\);
d) \({y^2} - \dfrac{3}{y} + 1\);
e) \(- 6z + 8\);
g) \(- 2{t^{2021}} + 3{t^{2020}} + t - 1\).
Đa thức một biến là tổng những đơn thức của cùng một biến. Mỗi đơn thức cũng là một đa thức.
Bậc của đa thức là số mũ cao nhất của biến có trong đa thức.
Các biểu thức là đa thức một biến là:
a) \(- 2x\) : biến là x và bậc của đa thức là 1.
b) \(- {x^2} - x + \dfrac{1}{2}\) : biến là x và bậc của đa thức là bậc 2.
e) \(- 6z + 8\) : biến là z và bậc của đa thức là bậc 1.
g) \(- 2{t^{2021}} + 3{t^{2020}} + t - 1\) : biến là t và bậc của đa thức là 2021.
52
Thực hiện mỗi phép tính sau:
a) \(\dfrac{4}{9}x + \dfrac{2}{3}x\);
b) \(- 12{y^2} + 0,7{y^2}\);
c) \(- 21{t^3} - 25{t^3}\).
Ta thực hiện các phép tính với biến có cùng số mũ. Giữ nguyên biến và thực hiện phép tính phần hệ số.
a) \(\dfrac{4}{9}x + \dfrac{2}{3}x = (\dfrac{4}{9} + \dfrac{2}{3})x = (\dfrac{4}{9} + \dfrac{6}{9})x = \dfrac{{10}}{9}x\);
b) \(- 12{y^2} + 0,7{y^2} = ( - 12 + 0,7){y^2} = - 11,3{y^2}\);
c) \(- 21{t^3} - 25{t^3} = ( - 21 - 25){t^3} = - 46{t^3}\).
52
Cho hai đa thức:
\(P(y) = - 12{y^4} + 5{y^4} + 13{y^3} - 6{y^3} + y - 1 + 9\);
\(Q(y) = - 20{y^3} + 31{y^3} + 6y - 8y + y - 7 + 11\).
a) Thu gọn mỗi đa thức trên rồi sắp xếp mỗi đa thức theo số mũ giảm dần của biến.
b) Tìm bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức.
a) Ta thực hiện phép cộng các đơn thức có cùng số mũ của biến x sao cho trong đa thức P(y), Q(y) không còn hai đơn thức nào có cùng số mũ của biến y.
Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến.
b) Bậc của đa thức là số mũ cao nhất của biến có trong đa thức. Hệ số cao nhất là hệ số đi cùng với biến có số mũ cao nhất trong đa thức. Hệ số tự do là hệ số không đi cùng biến hoặc đi cùng biến với số mũ là 0.
a)
\(P(y) = - 12{y^4} + 5{y^4} + 13{y^3} - 6{y^3} + y - 1 + 9 = ( - 12 + 5){y^4} + (13 - 6){y^3} + y + ( - 1 + 9)\)
\(= - 7{y^4} + 7{y^3} + y + 8\)
\(Q(y) = - 20{y^3} + 31{y^3} + 6y - 8y + y - 7 + 11 = ( - 20 + 31){y^3} + (6 - 8 + 1)y + ( - 7 + 11)\)
\(= 11{y^3} - y + 4\)
b) Đa thức P(y): bậc của đa thức là 4; hệ số cao nhất là – 7; hệ số tự do là 8.
Đa thức Q(y): bậc của đa thức là 3; hệ số cao nhất là 11; hệ số tự do là 4.
53
Cho đa thức \(P(x) = a{x^2} + bx + c\)(a ≠ 0). Chứng tỏ rằng:
a) \(P(0) = c\);
b) \(P(1) = a + b + c\);
c) \(P( - 1) = a - b + c\)
Muốn chứng tỏ các giá trị của a), b), c) đúng; ta thay giá trị của biến x vào đa thức để kiểm tra.
a) Thay x = 0 vào đa thức P(x) ta được:
\(P(0) = a{.0^2} + b.0 + c = 0 + 0 + c = c\). Vậy \(P(0) = c\).
b) Thay x = 1 vào đa thức P(x) ta được:
\(P(0) = a{.1^2} + b.1 + c = a + b + c\). Vậy \(P(1) = a + b + c\).
c) Thay x = – 1 vào đa thức P(x) ta được:
\(P(0) = a.{( - 1)^2} + b.( - 1) + c = a + ( - b) + c = a - b + c\). Vậy \(P( - 1) = a - b + c\).
53
Kiểm tra xem:
a) \(x = 2,x = \dfrac{4}{3}\) có là nghiệm của đa thức \(P(x) = 3x - 4\) hay không;
b) \(y = 1,y = 4\) có là nghiệm của đa thức \(Q(y) = {y^2} - 5y + 4\) hay không.
x = a là nghiệm của một đa thức khi và chỉ khi ta thay a vào đa thức, ta được giá trị của đa thức bằng 0.
a)
Thay \(x = 2\) vào đa thức \(P(x) = 3x - 4\) ta được: \(P(2) = 3.2 - 4 = 6 - 4 = 2\).
Thay \(x = \dfrac{4}{3}\) vào đa thức \(P(x) = 3x - 4\) ta được: \(P(\dfrac{4}{3}) = 3.\dfrac{4}{3} - 4 = 4 - 4 = 0\).
Vậy x = 2 không là nghiệm của đa thức \(P(x) = 3x - 4\); \(x = \dfrac{4}{3}\)là nghiệm của đa thức \(P(x) = 3x - 4\).
b) Thay \(y = 1\) vào đa thức \(Q(y) = {y^2} - 5y + 4\) ta được: \(Q(1) = {1^2} - 5.1 + 4 = 1 - 5 + 4 = 0\).
Thay \(y = 4\) vào đa thức \(Q(y) = {y^2} - 5y + 4\) ta được: \(Q(4) = {4^2} - 5.4 + 4 = 16 - 20 + 4 = 0\).
Vậy \(y = 1,y = 4\)là nghiệm của đa thức \(Q(y) = {y^2} - 5y + 4\).
53
Theo tiêu chuẩn của Tổ chức Y tế Thế giới (WHO), đối với bé giá, công thức tính cân nặng tiêu chuẩn là \(C = 9 + 2(N - 1)\) (kg), công thức tính chiều cao tiêu chuẩn là \(H = 75 + 5(N - 1)\) (cm), trong đó N là số tuổi của bé gái.
(Nguồn: http://sankom.vn)
a) Tính cân nặng chuẩn, chiều cao chuẩn của một bé gái 3 tuổi.
b) Một bé gái 3 tuổi nặng 13,5 kg và cao 86 cm. Bé gái đó có đạt tiêu chuẩn về cân nặng và chiều cao của Tổ chức Y tế Thế giới hay không?
a) Để tính cân nặng chuẩn, chiều cao chuẩn của một bé gái 3 tuổi, ta thay số tuổi của bé gái vào 2 công thức đã cho rồi thực hiện phép tính.
b) Muốn biết bé gái có đạt tiêu chuẩn về cân nặng và chiều cao của Tổ chức Y tế Thế giới hay không, ta so sánh với cân nặng chuẩn, chiều cao chuẩn đã tính được ở phần a.
a) Cân nặng chuẩn, chiều cao chuẩn của một bé gái 3 tuổi lần lượt là:
\(C = 9 + 2(3 - 1) = 9 + 2.2 = 13\)(kg);
\(H = 75 + 5(3 - 1) = 75 + 5.2 = 75 + 10 = 85\)(cm).
b) Ta thấy: 13,5 > 13 và 86 > 85. Vậy nên bé gái không đạt tiêu chuẩn (thừa tiêu chuẩn) về cân nặng và chiều cao của Tổ chức Y tế Thế giới.
53
Nhà bác học Galileo Galilei (1564 – 1642) là người đầu tiên phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian chuyển động. Quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) được biểu diễn gần đúng bởi công thức \(y = 5{x^2}\). Trong một thí nghiệm vật lí, người ta thả một vật nặng từ độ cao 180 m xuống đất (coi sức cản của không khí không đáng kể).
a) Sau 3 giây thì vật nặng còn cách mặt đất bao nhiêu mét?
b) Khi vật nặng còn cách mặt đất 100 m thì nó đã rơi được thời gian bao lâu?
c) Sau bao lâu thì vật chạm đất?
a) Thay t = 3 vào công thức rồi thực hiện phép tính để biết được sau 3 giây thì vật nặng đi được quãng đường là bao nhiêu. Rồi lấy độ cao người thả vật trừ đi.
b) Tính quãng đường mà vật nặng rơi được (lấy độ cao người thả vật trừ đi 100 m) rồi thay vào công thức để tính thời gian rơi của vật.
c) Để tính thời gian vật chạm đất ta lấy y = 180 m, tìm x.
a) Sau 3 giây, quãng đường chuyển động mà vật được thả rơi là:
\(y = {5.3^2} = 5.9 = 45\)(m)
Vậy sau 3 giây thì vật nặng còn cách mặt đất là:
\(180 - 45 = 135\)(m)
b) Khi vật nặng rơi cách mặt đất 100 m tức vật nặng đã rơi được:
\(180 - 100 = 80\)(m)
Khi vật nặng còn cách mặt đất 100 m thì nó đã rơi được khoảng thời gian là:
\(\begin{array}{l}80 = 5.{x^2}\\ \to {x^2} = 16\\ \to x = 4\end{array}\)
Vậy khi vật nặng còn cách mặt đất 100 m thì nó đã rơi được khoảng 4 (giây).
c) Khoảng thời gian để vật chạm đất là:
\(\begin{array}{l}180 = 5.{x^2}\\ \to {x^2} = 36\\ \to x = 6\end{array}\)
Vậy sau khoảng 6 giây thì vật chạm đất.
53
Pound là một đơn vị đo khối lượng truyền thống của Anh, Mỹ và một số quốc gia khác. Công thức tính khối lượng y (kg) theo x (pound) là: \(y = 0,45359237x\).
a) Tính giá trị của y (kg) khi x = 100 (pound).
b) Một hãng hàng không quốc tế quy định mỗi hành khách được mang hai va li không tính cước; mỗi va li cân nặng không vượt quá 23 kg. Hỏi với va li cân nặng 50,99 pound sau khi quy đổi sang ki-lô-gam và được phép làm tròn đến hàng đơn vị thì có vượt quá quy định trên hay không?
a) Thay giá trị của x vào công thức rồi thực hiện phép tính.
b) Muốn kiểm tra xem va li có vượt quá quy định hay không, ta thay cân nặng của va li vào công thức rồi thực hiện phép tính. Sau đó, so sánh với quy định của hãng hàng không.
a) Giá trị của y (kg) khi x = 100 (pound) là:
\(y = 0,45359237.100 = 45,359237\)(kg).
b) Với ca li cân nặng 50,99 pound khi đổi ra ki-lô-gam là:
\(y = 0,45359237.50,99 = 23,1286749463 \approx 23\)(kg)
Quy định của hãng hàng không quốc tế là mỗi va li cân nặng không quá 23 kg. Và với va li cân nặng 50,99 pound khi đổi ra ki-lô-gam và được làm tròn đến hàng đơn vị là 23 kg.
Vậy với va li cân nặng 50,99 pound thì không vượt quá quy định của hãng hàng không.
