Khởi động
112
Hình 121 minh họa biển giới thiệu quần thể di tích, danh thắng cấp Quốc gia núi Dũng Quyết và khu vực Phượng Hoàng Trung Đô ở tỉnh Nghệ An (Hình 120).

Làm thế nào để xác định được vị trí cách đều ba địa điểm được minh họa trong Hình 121?
Gợi ý
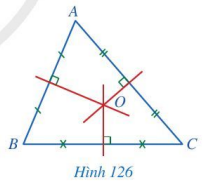
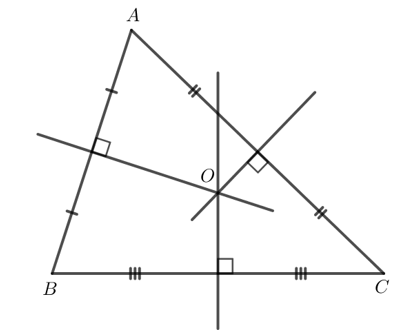
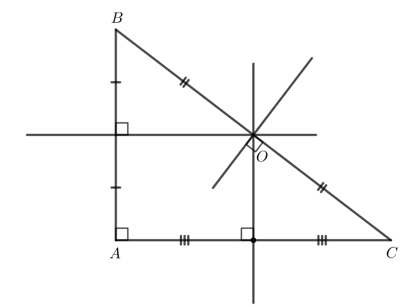
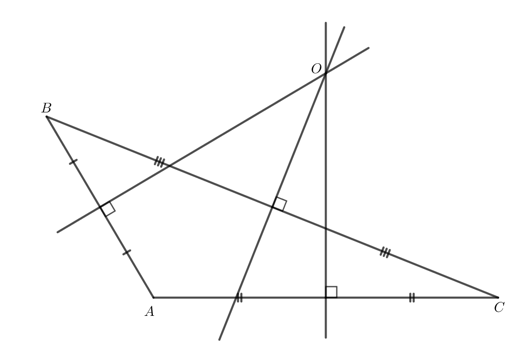
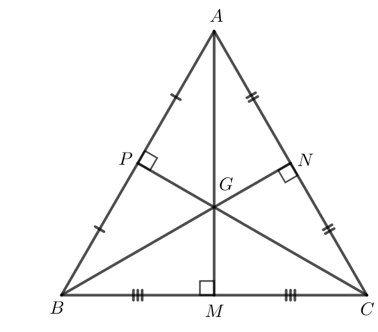
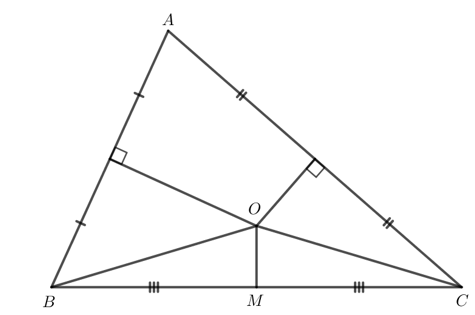
Dựa vào : Tính chất của ba đường trung trực trong tam giác
Đáp án
Để xác định được vị trí cách đều ba địa điểm được minh họa trong Hình 121, ta xác định ba đường trung trực của tam giác được tạo thành từ ba đỉnh đó rồi xác định giao điểm của đường trung trực đó.