5
Nhiệt độ lúc 13 giờ ngày 24/01/2016 tại một số trạm đo được bởi bảng như sau:
Các số chỉ nhiệt độ nêu trên có viết được dưới dạng phân số không?
Viết số thập phân dưới dạng phân số có mẫu số là lũy thừa của 10 như đã học
Các số chỉ nhiệt độ nêu trên có viết được dưới dạng phân số. Cụ thể:
5
Viết các số -3; 0,5; \(2\frac{3}{7}\) dưới dạng phân số
Biểu diễn số nguyên a dưới dạng phân số \(\frac{a}{1}\)
Số thập phân dưới dạng phân số có mẫu số là lũy thừa của 10.
Hỗn số dương \(a\frac{b}{c} = \frac{{a.c + b}}{c}\)
Ta có:
\(\begin{array}{l} - 3 = \frac{{ - 3}}{1};\\0,5 = \frac{5}{{10}} = \frac{1}{2};\\2\frac{3}{7} = \frac{{2.7 + 3}}{7} = \frac{{17}}{7}\end{array}\)
6
Các số 21; -12; \(\frac{{ - 7}}{{ - 9}}\); -4,7; -3,05 có là số hữu tỉ không? Vì sao?
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}(a,b \in Z,b \ne 0)\).
Các số 21; -12; \(\frac{{ - 7}}{{ - 9}}\); -4,7; -3,05 có là số hữu tỉ vì chúng đều viết được dưới dạng phân số\(21 = \frac{{21}}{1}; - 12 = \frac{{ - 12}}{1};\frac{{ - 7}}{{ - 9}} = \frac{7}{9}; - 4,7 = \frac{{ - 47}}{{10}}; - 3,05 = \frac{{ - 305}}{{100}} = \frac{{ - 61}}{{20}}\)
6
Biểu diễn số hữu tỉ \(\frac{7}{{10}}\) trên trục số
Chia đoạn thẳng đơn vị thành 10 phần bằng nhau. Lấy một đoạn làm đơn vị mới ( đơn vị mới bằng \(\frac{1}{{10}}\) đơn vị cũ)
Số hữu tỉ \(\frac{7}{{10}}\) được biểu diễn bằng điểm nằm bên phải gốc O, cách gốc O một đoạn bằng 7 đơn vị mới.
7
Biểu diễn số hữu tỉ -0,3 trên trục số
Viết các số hữu tỉ dưới dạng phân số: -0,3 = - \(\frac{3}{{10}}\)
Chia đoạn thẳng đơn vị thành 10 phần bằng nhau. Lấy một đoạn làm đơn vị mới ( đơn vị mới bằng \(\frac{1}{{10}}\) đơn vị cũ)
Số hữu tỉ -\(\frac{3}{{10}}\) được biểu diễn bằng điểm nằm bên trái gốc O, cách gốc O một đoạn bằng 3 đơn vị mới.
7
Quan sát hai điểm biểu diễn các số hữu tỉ \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\) trên trục số sau:
Nêu nhận xét về khoảng cách từ hai điểm \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\) đến điểm 0.
So sánh khoảng cách từ hai điểm \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\) đến điểm 0.
Hai điểm biểu diễn các số hữu tỉ \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\) cách gốc 0 một khoảng bằng nhau.
8
Tìm số đối của mỗi số sau: \(\frac{2}{9}; - 0,5\)
Số đối của số hữu tỉ \(\frac{a}{b}\) là số hữu tỉ \(\frac{{ - a}}{b}\).
Số đối của \(\frac{2}{9}\) là - \(\frac{2}{9}\)
Số đối của -0,5 là 0,5
9
So sánh:
a) \(- \frac{1}{3}\) và \(\frac{{ - 2}}{5}\)
b) 0,125 và 0,13
c) -0,6 và \(\frac{{ - 2}}{3}\)
a) Đưa 2 phân số về dạng cùng mẫu số dương rồi so sánh tử số của 2 phân số: Phân số nào có tử số lớn hơn thì lớn hơn
b) So sánh 2 số thập phân: So sánh các hàng tương ứng từ trái qua phải của 2 số thập phân
c) Viết chúng dưới dạng phân số rồi so sánh 2 phân số
a) Ta có:
\(- \frac{1}{3} = \frac{{ - 5}}{{15}};\frac{{ - 2}}{5} = \frac{{ - 6}}{{15}}\)
Vì -5 > -6 nên \(\frac{{ - 5}}{{15}} > \frac{{ - 6}}{{15}}\) hay \(- \frac{1}{3}\) > \(\frac{{ - 2}}{5}\)
b) 0,125 < 0,13 vì chữ số hàng phần trăm của 0,125 là 2 nhỏ hơn chữ số hàng phần trăm của 0,13 là 3
c) Ta có:
\(\begin{array}{l} - 0,6 = \frac{{ - 6}}{{10}} = \frac{{ - 3}}{5} = \frac{{ - 9}}{{15}};\\\frac{{ - 2}}{3} = \frac{{ - 10}}{{15}}\end{array}\)
Vì -9 > -10 nên \(\frac{{ - 9}}{{15}} > \frac{{ - 10}}{{15}}\) hay - 0,6 > \(\frac{{ - 2}}{3}\)
9
So sánh:
a) -3,23 và -3,32
b) \(- \frac{7}{3}\) và -1,25
a) So sánh 2 số thập phân dương: So sánh các hàng tương ứng từ trái qua phải của 2 số thập phân
Nếu a > b thì – a < - b
b) Viết chúng dưới dạng phân số rồi so sánh 2 phân số
a) Ta có: 3,23 < 3,32 nên -3,23 > -3,32
b) Ta có: \(- \frac{7}{3} = \frac{{ - 28}}{{12}}; - 1,25 = \frac{{ - 125}}{{100}} = \frac{{ - 5}}{4} = \frac{{ - 15}}{{12}}\)
Vì -28 < -15 nên \(\frac{{ - 28}}{{12}} < \frac{{ - 15}}{{12}}\) hay \(- \frac{7}{3}\) < -1,25
9
Giả sử hai điểm a, b lần lượt biểu diễn hai số nguyên a,b trên trục số nằm ngang. Với a < b, nêu nhận xét về vị trí của điểm a so với điểm b trên trục số đó.
Biểu diễn 2 số nguyên trên trục số nằm ngang
Nếu a < b thì điểm a nằm bên trái điểm b trên trục số
Chú ý: Nhận xét: Trên trục số nằm ngang, điểm biểu diễn số hữu tỉ nhỏ hơn nằm bên trái điểm biểu diễn số hữu tỉ lớn hơn.
10
Các số 13, -29; -2,1; 2,28; \(\frac{{ - 12}}{{ - 18}}\) có là số hữu tỉ không? Vì sao?
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}(a,b \in Z,b \ne 0)\)
Các số 13, -29; -2,1; 2,28; \(\frac{{ - 12}}{{ - 18}}\) có là số hữu tỉ vì:
\(13 = \frac{{13}}{1}; - 29 = \frac{{ - 29}}{1}; - 2,1 = \frac{{-21}}{{10}};2,28 = \frac{{228}}{{100}} = \frac{{54}}{{25}};\frac{{ - 12}}{{ - 18}} = \frac{2}{3}\)
Chú ý: Một số nguyên cũng là một số hữu tỉ.
10
Chọn kí hiệu thích hợp cho dấu “?”
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}(a,b \in Z,b \ne 0)\)
Dùng kí hiệu “\( \in \)” nếu số thuộc tập hợp
Dùng kí hiệu “\( \notin \)” nếu số không thuộc tập hợp
10
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Nếu \(a \in \mathbb{N}\) thì \(a \in \mathbb{Q}\)
b) Nếu \(a \in \mathbb{Z}\) thì \(a \in \mathbb{Q}\)
c) Nếu \(a \in \mathbb{Q}\) thì \(a \in \mathbb{N}\)
d) Nếu \(a \in \mathbb{Q}\) thì \(a \in \mathbb{Z}\)
e) Nếu \(a \in \mathbb{N}\) thì \(a \notin \mathbb{Q}\)
g) Nếu \(a \in \mathbb{Z}\) thì \(a \notin \mathbb{Q}\)
Tập hợp các số hữu tỉ \(\mathbb{Q} = \left\{ {\frac{a}{b};\,a,b \in \mathbb{Z};\,b \ne 0} \right\}\)
\(\mathbb{N} = \left\{ {0;\,1;\,2;...} \right\}\)
\(\mathbb{Z} = \left\{ {..., - 2; - 1;0;\,1;\,2;...} \right\}\)
a) Nếu \(a \in \mathbb{N}\) thì \(a \in \mathbb{Q}\) => Đúng
b) Nếu \(a \in \mathbb{Z}\) thì \(a \in \mathbb{Q}\) => Đúng
c) Nếu \(a \in \mathbb{Q}\) thì \(a \in \mathbb{N}\) => Sai. Vì a là số hữu tỉ thì chưa chắc a là số tự nhiên.
d) Nếu \(a \in \mathbb{Q}\) thì \(a \in \mathbb{Z}\) => Sai. Vì a là số hữu tỉ thì chưa chắc a là số nguyên.
e) Nếu \(a \in \mathbb{N}\) thì \(a \notin \mathbb{Q}\) => Sai. Vì các số tự nhiên là các số hữu tỉ
g) Nếu \(a \in \mathbb{Z}\) thì \(a \notin \mathbb{Q}\) => Sai. Vì các số nguyên là các số hữu tỉ
11
Quan sát trục số sau và cho biết các điểm A, B, C, D biểu diễn những số nào?
- Điểm biểu diễn số hữu tỉ a là điểm a.
- Quan vị trí các điểm A, B, C, D trên trục số và trả lời câu hỏi.
- Các điểm A, B, C, D biểu diễn lần lượt các số: \(- \frac{9}{7}; - \frac{3}{7};\frac{2}{7};\frac{6}{7}\)
11
Tìm số đối của mỗi số sau: \(\frac{9}{{25}};\,\frac{{ - 8}}{{27}};\, - \frac{{15}}{{31}};\frac{5}{{ - 6}};\,3,9;\, - 12,5\).
Số đối của số x kí hiệu là: -x
Số đối của các số \(\frac{9}{{25}};\,\frac{{ - 8}}{{27}};\, - \frac{{15}}{{31}};\frac{5}{{ - 6}};\,3,9;\, - 12,5\) lần lượt là:
\( - \frac{9}{{25}};\,\frac{8}{{27}};\,\frac{{15}}{{31}};\frac{5}{6};\, - 3,9;\,12,5\).
11
Biểu diễn số đối của mỗi số đã cho trên trục số sau:
Số đối của một số a nằm bên kia số 0 và cách 0 một khoảng bằng với khoảng cách từ điểm a đến điểm 0.
Số đối của \(\dfrac{-5}{6}\) là \(\dfrac{5}{6}\)
Số đối của \(\dfrac{-1}{3}\) là \(\dfrac{1}{3}\)
Số đối của \(0\) là \(0\)
Số đối của \(1\) là \(-1\)
Số đối của \(\dfrac{7}{6}\) là \(\dfrac{-7}{6}\)
11
So sánh:
a) \(2,4\) và \(2\frac{3}{5}\);
b) \(- 0,12\) và \(- \frac{2}{5}\)
c)\(\frac{{ - 2}}{7}\) và \(- 0,3\).
Đưa các số về dạng hai phân số cùng mẫu rồi so sánh.
a)\(2,4 =\frac{24}{10}=\frac{{12}}{5}\) và \(2\frac{3}{5} = \frac{{13}}{5}\)
Ta có: \(\frac{{12}}{5} < \frac{{13}}{5} \Rightarrow 2,4 < 2\frac{3}{5}\).
b) \(- 0,12 = -\frac{12}{100}= - \frac{3}{{25}}\) và \(- \frac{2}{5} = - \frac{{10}}{{25}}\)
Ta có: -3 > -10 nên \(- \frac{3}{{25}} > - \frac{{10}}{{25}}\) nên \(- 0,12 > - \frac{2}{5}\).
c)\(\frac{{ - 2}}{7} = \frac{{ - 20}}{{70}}\) và \(- 0,3 = \frac{{ - 3}}{{10}} = \frac{{ - 21}}{{70}}\).
Do -20 > -21 nên \(\frac{{ - 20}}{{70}} > \frac{{ - 21}}{{70}}\) nên \(\frac{{ - 2}}{7} > - 0,3.\)
11
a) Sắp xếp các số sau theo thứ tự tăng dần: \(\frac{{ - 3}}{7};\,0,4;\, - 0,5;\,\frac{2}{7}\).
b) Sắp xếp các số sau theo thứ tự giảm dần: \(\frac{{ - 5}}{6};\, - 0,75;\, - 4,5;\, - 1\).
-Đưa các số về các phân số có cùng mẫu số để so sánh
-Sắp xếp các phân số theo thứ tự.
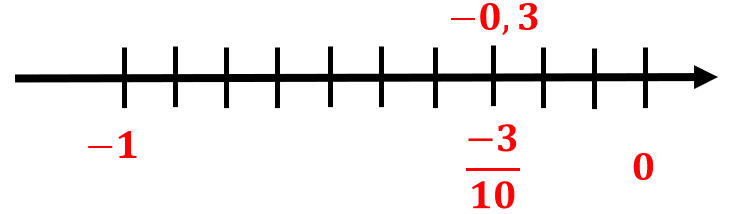
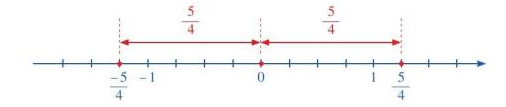
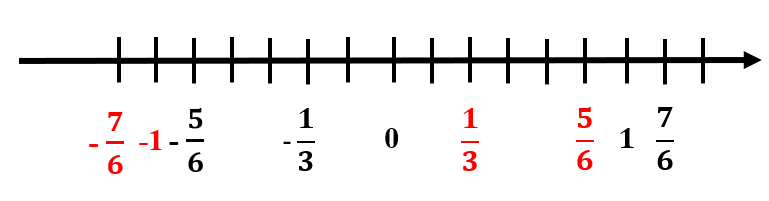
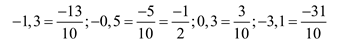a) Ta có:
\(\begin{array}{l}\frac{{ - 3}}{7} = \frac{{ - 6}}{{14}} ; \frac{{ - 1}}{2}=\frac{{ - 7}}{{14}} ;\frac{2}{5} = \frac{{14}}{{35}};\frac{2}{7}=\frac{{10}}{{35}} \end{array}\)
Vì -7 < -6 < 0 nên \(\frac{{ - 7}}{{14}}<\frac{{ - 6}}{{14}}<0\)
Vì 0<10<14 nên \(0<\frac{{10}}{{35}}<\frac{{14}}{{35}}\)
Do đó: \(\frac{{ - 7}}{{14}} < \frac{{ - 6}}{{14}} < \frac{{10}}{{35}} < \frac{{14}}{{35}}\)
=> Sắp xếp các số theo thứ tự tăng dần: \(\frac{{ - 1}}{2};\,\frac{{ - 3}}{7};\,\frac{2}{7};\frac{2}{5}\)
b) Ta có: \(\frac{{ - 5}}{6} = - 0,8\left( 3 \right)\)
Mà \(- 0,75 > - 0,8\left( 3 \right) > - 1 > - 4,5\).
=>Sắp xếp các số theo thứ tự giảm dần: \(- 0,75;\frac{{ - 5}}{6}; - 1; - 4,5\)
11
Hình 4 mô tả một chiếc cân khối lượng, ở đó các vạch ghi 46 và 48 lần lượt ứng với các số đo 46 kg và 48 kg. Khi nhìn vị trí mà chiếc kim chỉ vào, bạn Minh đọc số đo là 47,15 kg, bạn Dương đọc số đo là 47,3 kg, bạn Quân đọc số đo là 47,65 kg. Bạn nào đã đọc đúng số đo? Vì sao?
Quan sát độ chia nhỏ nhất của chiếc cân và quan sát xem chiếc kim chỉ vào số bao nhiêu
Ta thấy độ chia nhỏ nhất là 100g, chiếc kim chỉ quá số 47 ba vạch chia nhỏ nhất nên nó chỉ số 47,3kg.
Vậy bạn Dương đọc đúng, bạn Minh và Quân đọc sai.
11
Cô Hạnh dự định xây tầng hầm cho ngôi nhà của gia đình. Một công ty tư vấn xây dựng đã cung cấp cho cô Hạnh lựa chọn một trong sáu số đo chiều cao của tầng hầm như sau: 2,3 m; 2,35 m; 2,4 m; 2,55 m; 2,5 m; 2,75 m. Cô Hạnh dự định chọn chiều cao của tầng hầm lớn hơn \(\frac{{13}}{5}\)m để đảm bảo ánh sáng, thoáng đãng, cân đối về kiến trúc và thuận tiện trong sử dụng. Em hãy giúp cô Hạnh chọn đúng số đo chiều cao của tầng hầm.
Đổi chiều cao của tầng hầm ra số thập phân rồi so sánh với sáu số đo chiều cao được tư vấn.
=>Chọn chiều cao lớn hơn chiều cao của tầng hầm.
