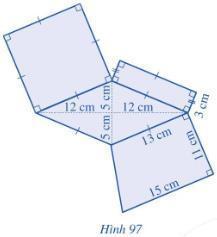
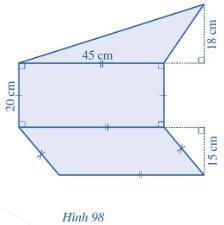
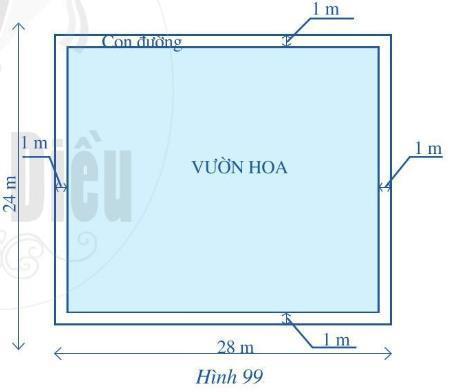
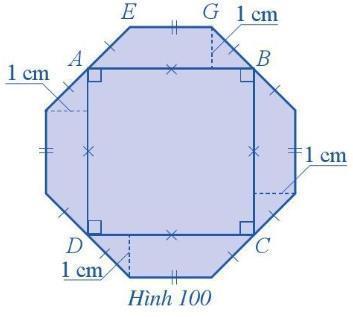
Bài tập 1
117
Tạo ra hình hộp có nắp
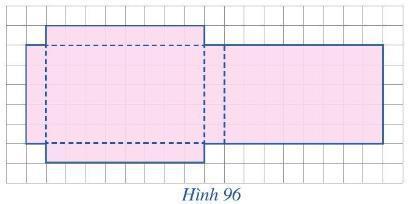
Hãy vẽ của hình chữ nhật trên một miếng bìa (mỏng) theo cách như ở Hình 96, sau đó cắt, gấp lại và dán mép để tạo ra hình hộp có nắp.
Gợi ý
Chuẩn bị miếng bìa, bút thước và kéo.
Đáp án
Kẻ các nét đứt và nét liền như hình vẽ.
Cắt miếng bìa theo mép ngoài cùng như hình vẽ.
Gấp miếng bìa theo các nét đứt về hướng miếng bìa hình chữ nhật lớn ở bên phải ta được một hình hộp có nắp.