Hoạt động 1
76
Tính và so sánh kết quả: \(7 - 2\) và \(7 + \left( { - 2} \right)\).
Gợi ý
Thực hiện các phép tính và so sánh các kết quả.
Đáp án
7 – 2 = 5
7 + ( - 2) = 7-2=5
Vậy: 7 – 2 = 7 + (- 2)
Bài 4: Phép trừ các số nguyên. Quy tắc dấu ngoặc
Luyện tập vận dụng 1
77
Nhiệt độ lúc 17 giờ là \(5^\circ C\), đến 21 giờ nhiệt độ giảm đi \(6^\circ C\). Viết phép tính và tính nhiệt độ lúc 21 giờ.
Gợi ý
- Nhiệt độ giảm: Phép trừ.
- Quy tắc phép trừ: \(a - b = a + \left( { - b} \right)\).
Đáp án
Nhiệt độ lúc 21 giờ giảm đi \(6^\circ C\) nên còn: \(5 - 6 = 5 + \left( { - 6} \right) = - \left( {6 - 5} \right) = - 1\left( {^\circ C} \right)\).
Vậy nhiệt độ lúc 21 giờ là \( - 1^\circ C\).
Hoạt động 2
77
Tính và so sánh kết quả trong mỗi trường hợp sau:
a) 5 + (8 + 3) và 5 + 8 + 3.
b) 8 + (10 – 5) và 8 + 10 – 5.
c) 12 – (2 + 16) và 12 – 2 + 16.
d) 18 – (5 – 15) và 18 – 5 + 15.
Gợi ý
Tính và so sánh kết quả
Đáp án
a) 5 + (8 + 3) = 5 + 11 = 16.
5 + 8 + 3 = 13 + 3 = 16.
Vậy 5 + (8 + 3) = 5 + 8 + 3.
b) 8 + (10 – 5) = 8 + 5 = 13.
8 + 10 – 5 = 18 – 5 = 13.
Vậy 8 + (10 – 5) = 8 + 10 – 5.
c) 12 – (2 + 16) = 12 – 18 = – (18 – 12)= – 6.
12 – 2 – 16 = 10 – 16 = – 6.
Vậy 12 – (2 + 16) = 12 – 2 + 16.
d) 18 – (5 – 15) = 18 - 5 + 15 = 18 + 10 = 28.
18 – 5 + 15 = 13 + 15 = 28.
Vậy 18 – (5 – 15) = 18 – 5 + 15.
Luyện tập vận dụng 2
78
Tính một cách hợp lí:
a) (- 215) + 63 + 37
b) (- 147) – (13 - 47).
Gợi ý
a) - Tính tổng 63 + 37 trước.
- Sử dụng quy tắc cộng hai số nguyên trái dấu.
b) – Bỏ dấu ngoặc: Trước dấu ngoặc có dấu “–” , ta đổi dấu của số hạng trong ngoặc: dấu “+” thành dấu “– ” và ngược lại.
– Trừ số nguyên: \(a + b = a + \left( { - b} \right)\)
Đáp án
a) (– 215) + 63 + 37
= (– 215) + (63 + 37)
= (– 215) + 100
= – (215–100)
= – 115.
b) (– 147) – (13 – 47)
= (– 147) – 13 + 47
= [(– 147) + 47] – 13
= – (147 – 47) – 13
= – 100 – 13
= – 113
Bài tập 1
78
Tính:
a) \(\left( { - 10} \right) - 21 - 18\)
b) \(24 - \left( { - 16} \right) + \left( { - 15} \right)\)
c) \(49 - \left[ {15 + \left( { - 6} \right)} \right]\)
d) \(\left( { - 44} \right) - \left[ {\left( { - 14} \right) - 30} \right]\)
Gợi ý
– Bỏ dấu ngoặc: Trước dấu ngoặc có dấu “–” , ta đổi dấu của số hạng trong ngoặc: dấu “+” thành dấu “– ” và ngược lại.
– Trừ số nguyên: \(a + b = a + \left( { - b} \right)\)
Đáp án
a) \(\left( { - 10} \right) - 21 - 18\)
\(\begin{array}{l} = \left( { - 10} \right) + \left( { - 21} \right) - 18\\ =- \left( {10 + 21} \right) +(-18)\\ =\left( { - 31} \right) +(-18)\\ =- \left( {31 + 18} \right)\\ =- 49\end{array}\)
b) \(24 - \left( { - 16} \right) + \left( { - 15} \right)\)
\(\begin{array}{l} = 24 + 16 + \left( { - 15} \right)\\ = \left( {24 + 16} \right) + \left( { - 15} \right)\\ = 40 + \left( { - 15} \right)\\ = 40 - 15\\ = 25\end{array}\)
c) \(49 - \left[ {15 + \left( { - 6} \right)} \right]\)
\(\begin{array}{l} = 49 - \left[ {15 - 6} \right]\\ = 49 - 9\\ = 40\end{array}\)
d) \(\left( { - 44} \right) - \left[ {\left( { - 14} \right) - 30} \right]\)
\(\begin{array}{l} = \left( { - 44} \right) + 14 + 30\\ =- \left( {44 - 14} \right) + 30\\ =- 30 + 30\\ = 0\end{array}\)
Bài tập 2
78
Tính một cách hợp lí:
a) \(10 - 12 - 8\).
b) \(4 - \left( { - 15} \right) - 5 + 6\).
c) \(2 - 12 - 4 - 6\).
d)\(- 45 - 5 - \left( { - 12} \right) + 8\).
Gợi ý
a) - Đưa 12 và 8 vào trong ngoặc rồi đặt dấu “ – ” trước dấu ngoặc.
- Tính tổng trong ngoặc.
- Lấy 10 trừ đi kết quả trong ngoặc.
b) - Nhóm 4 và 6, số \(- \left( { - 15} \right)\) và \(- 5\) có dấu “ – ” ngoài cùng nên ta đặt dấu “ – ” ra ngoài và đổi dấu của \(- \left( { - 15} \right)\) và \(- 5\) thành \(+ \left( { - 15} \right)\) và \(+ 5\).
- Lưu ý: \(+ \left( { - 15} \right) = \left( { - 15} \right)\).
- Trừ cho một số nguyên là cộng với số đối của số nguyên đó.
c) - Nhóm 2 và \(- 12\) vào trong ngoặc, số \(- 4\) và \(- 6\) có dấu “ – ” ngoài cùng nên ta đặt dấu “ – ” ra ngoài và đổi dấu của \(- 4\) và \(- 6\) thành \(4\) và \(+ 6\).
- Trừ cho một số nguyên là cộng với số đối của số nguyên đó.
d) - Nhóm \(- 45\) và \(- 5\)
- Đổi dấu: \(- \left( { - 12} \right) = + 12\).
- Nhóm \(12 + 8\).
- Sử dụng quy tắc cộng hai số nguyên khác dấu.
Đáp án
a) \(10 - 12 - 8\)
\(\begin{array}{l} = 10 - \left( {12 + 8} \right)\\ = 10 - 20\\ =- \left( {20 - 10} \right)\\ =- 10\end{array}\)
b) \(4 - \left( { - 15} \right) - 5 + 6\)
\(= 4 + 15 -5 + 6= (4+6) + (15 - 5)=10+10 = 20\)
c) \(2 - 12 - 4 - 6\)
\(\begin{array}{l} = \left( {2 - 12} \right) - \left( {4 + 6} \right)\\ =- 10 - 10\\ =- \left( {10 + 10} \right)\\ =- 20\end{array}\)
d)\(- 45 - 5 - \left( { - 12} \right) + 8\)
\(\begin{array}{l} =- \left( {45 + 5} \right) + 12 + 8\\ =- 50 + \left( {12 + 8} \right)\\ =- 50 + 20\\ =- \left( {50 - 20} \right)\\ =- 30\end{array}\)
Bài tập 3
78
Tính giá trị biểu thức:
a) \(\left( { - 12} \right) - x\) với \(x = -28\);
b) \(a - b\) với \(a = 12,b = - 48\).
Gợi ý
a) - Thay \(x = 28\) vào x ở \(\left( { - 12} \right) - x\).
- Lấy \(\left( { - 12} \right)\) cộng với số đối của -28.
b) - Thay \(a = 12,b = - 48\) vào \(a - b\).
- Lấy 12 cộng với số đối của \(- 48\).
Đáp án
a) Thay \(x = -28\) vào \(\left( { - 12} \right) - x\), ta được:
\(\begin{array}{l}\left( { - 12} \right) - x\\ = \left( { - 12} \right) - (-28)\\ = \left( { - 12} \right) + 28\\ =28-12\\= 16\end{array}\)
b) Thay \(a = 12,b = - 48\) vào \(a - b\), ta được:
\(\begin{array}{l}a - b\\ = 12 - \left( { - 48} \right)\\ = 12 + 48\\ = 60\end{array}\)
Bài tập 4
78
Nhiệt độ lúc 6 giờ là \( - 3^\circ C\), đến 12 giờ nhiệt độ tăng \(10^\circ C\), đến 20 giờ nhiệt độ lại giảm \(8^\circ C\). Nhiệt độ lúc 20 giờ là bao nhiêu?
Gợi ý
- Nhiệt độ tăng là phép cộng, giảm là phép trừ.
- Lấy \( - 3^\circ C\) cộng \(10^\circ C\) rồi trừ \(8^\circ C\).
Đáp án
Nhiệt độ lúc 20 giờ là:
\(\begin{array}{l}\left( { - 3} \right) + 10 - 8\\ = 7 - 8\\ =- 1\left( {^\circ C} \right)\end{array}\)
Vậy nhiệt độ lúc 20 giờ là \(- 1^\circ C\).
Bài tập 5
78
Dùng máy tính cầm tay để tính:
56 – 182;
346 – (- 89);
(-76) – (103).
Gợi ý
Đáp án
\(56 - 182 = - 126\)
\(346 - \left( { - 89} \right) = 435\)
\(\left( { - 76} \right) - \left( {103} \right) = - 179\)
Bài tập 6
79
Đố vui. Em hãy dựa vào thông tin mỗi bức ảnh để tính tuổi của các nhà bác học sau:
Gợi ý
Năm trước công nguyên: Số âm.
Năm 212 trước công nguyên: \( - 212\)
Năm 287 trước công nguyên: \( - 287\)
Năm 495 trước công nguyên: \( - 495\)
Năm 570 trước công nguyên: \( - 570\)
Tuổi = Năm mất (số sau)-năm sinh (số trước).
Đáp án
+ Tuổi của nhà bác học Archimedes:
\(\left( { - 212} \right) - \left( { - 287} \right) = \left( { - 212} \right) + 287 = 287 - 212 = 75\)tuổi.
+ Tuổi của nhà bác học Pythagoras:
\(\begin{array}{l}\left( { - 495} \right) - \left( { - 570} \right)\\ = \left( { - 495} \right) + 570\\ = 570 - 495\\ = 75\end{array}\)
Vậy nhà bác học Archimedes 75 tuổi và nhà bác học Pythagoras 75 tuổi.
Tìm tòi - Mở rộng
79
Múi giờ của các vùng trên thế giới
Bản đồ sau cho biết múi giờ của các vùng trên thế giới. Việt Nam ở múi giờ + 7.
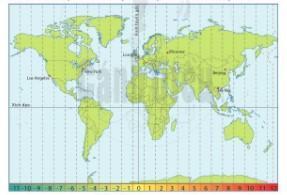
a) Xác định múi giờ của các thành phố sau: Bắc Kinh (Beijing), Mát-xcơ-va (Moscow), Luân Đôn (London), Niu Oóc (New York), Lốt An-giơ-lét (Los Angeles).
b) Cho biết Hà Nội và mỗi thành phố sau cách nhau bao nhiêu giờ: Bắc Kinh, Mát-xcơ-va, Luân Đôn, Niu Oóc, Lốt An-giơ-lét.
c) Biết thời gian ở Hà Nội đang là 8 giờ sáng, hãy tính giờ ở Bắc Kinh, Mát-xcơ-va, Luân Đôn, Niu Oóc, Lốt An-giơ-lét.
Gợi ý
Số giờ cách nhau của 2 nơi là hiệu 2 múi giờ của chúng
Đáp án
a) Múi giờ của các thành phố:
+) Bắc Kinh là: + 8
+) Mát-xcơ-va là: + 3
+) Luân Đôn là: 0
+) Niu Y-oóc là: – 5
+) Lốt An-giơ-lét là: – 8
b) Hà Nội cách Bắc Kinh số giờ là: (+ 8) – (+ 7) = 1 (giờ)
Hà Nội cách Mát-xcơ-va số giờ là: (+ 3) – (+ 7) = – 4 (giờ)
Hà Nội cách Luân Đôn số giờ là: 0 – (+ 7) = – 7 (giờ)
Hà Nội cách Niu Y-oóc số giờ là: (– 5) – (+ 7) = – 12 (giờ)
Hà Nội cách Lốt An-giơ-lét là: (– 8) – (+ 7) = – 15 (giờ)
c) Thời gian ở Hà Nội đang là 8 giờ sáng, khi đó:
Giờ ở Bắc Kinh là: 8 + 1 = 9 giờ sáng
Giờ ở Mát-xcơ-va là: 8 + (– 4) = 4 giờ sáng
Giờ ở Luân Đôn là: 8 + (– 7) = 1 giờ sáng
Giờ ở Niu Y-oóc là: 8 + (– 12) = – 4 giờ sáng, hay là 21 giờ đêm ngày hôm trước
Giờ ở Lốt An-giơ-lét là: 8 + (– 15) = – 7 giờ sáng, hay là 18 giờ tối ngày hôm trước.