93
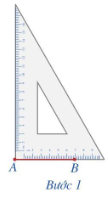
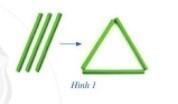
Hãy xếp ba chiếc que có độ dài bằng nhau để tạo thành Hình 1. Tam giác đó gọi là tam giác đều.
Sắp xếp ba que thành hình như mẫu.
- Đặt 2 chiếc que ở đỉnh sao cho đầu của 2 chiếc chạm vào nhau.
- Cố định vị trí chạm nhau của 2 chiếc que và đặt chiếc thứ 3 vào đầu còn lại của 2 chiếc que như trên hình.
93
Với tam giác đều ABC như ở Hình 2, thực hiện hoạt động sau:
a) Gấp tam giác ABC sao cho cạnh AB trùng với cạnh AC, đỉnh B trùng với đỉnh C ( Hình 3a). So sánh cạnh AB và cạnh AC, góc ABC và góc ACB.
b) Gấp tam giác ABC sao cho cạnh BC trùng với cạnh BA, đỉnh C trùng với đỉnh A ( Hình 3b). So sánh cạnh BC và cạnh BA; góc BCA và góc BAC.
Làm các bước như đề bài hướng dẫn và trả lời câu hỏi
a) Cắt sẵn hình tam giác đều:
Cạnh AB bằng cạnh AC.
Góc ABC bằng góc ACB.
b) Cạnh BC bằng cạnh BA.
Góc BCA bằng góc BAC.
94
Vẽ tam giác đều bằng thước và compa khi biết độ dài các cạnh.
Vẽ tam giác đều có cạnh tùy ý bằng thước và compa.
Ví dụ: Dùng thước và compa vẽ tam giác đều ABC có độ dài cạnh bằng 3cm.
Bước 1. Dùng thước vẽ đoạn thẳng AB = 3 cm.
Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.
Bước 3. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.
Bước 4. Dùng thước vẽ các đoạn thẳng AC và BC.
94
Hãy dùng thước và compa vẽ tam giác đều EGH có độ dài cạnh bằng 4 cm.
Nêu các bước và dùng thước và compa vẽ tam giác đều EGH có độ dài cạnh bằng 4 cm.
Bước 1. Dùng thước vẽ đoạn thẳng EG = 4 cm.
Bước 2. Lấy E làm tâm, dùng compa vẽ một phần đường tròn có bán kính EG.
Bước 3. Lấy G làm tâm, dùng compa vẽ một phần đường tròn có bán kính GE; gọi H là giao điểm của hai phần đường tròn vừa vẽ.
Bước 4. Dùng thước vẽ các đoạn thẳng EH và GH.
94
Với hình vuông HKLM ở hình 5, thực hiện hoạt động sau:
a) Đếm số ô vuông để so sánh độ dài các cạnh HK, KL, LM, MH
b) Quan sát xem các cạnh đối HK và ML, HM và KL của hình vuông HKLM có song song với nhau không.
c) Đếm số ô vuông để so sánh độ dài hai đường chéo KM và HL.
d) Nêu đặc điểm bốn góc ở các tỉnh H, K, L, M.
Quan sát hình đã cho và trả lời câu hỏi
a) Độ dài các cạnh HK, KL, LM, MH bằng nhau và đều bằng 4 ô vuông.
b) Các cạnh đối HK và ML, HM và KL của hình vuông HKLM song song với nhau.
c) Độ dài đường chéo KM và HL bằng nhau và đều đi qua 4 ô vuông.
d) Bốn góc ở các đỉnh H, K, L, M là các góc vuông.
95
Vẽ bằng ê ke hình vuông EGHI có độ dài cạnh bằng 6cm.
Vẽ bằng ê ke hình vuông EGHI có độ dài cạnh bằng 6cm.
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng EG có độ dài bằng 6cm.
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm E và một cạnh ê ke nằm trên EG, vẽ theo cạnh kia của ê ke đoạn thẳng EI có độ dài bằng 6 cm.
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh GH có độ dài bằng 6 cm.
Bước 4. Vẽ đoạn thẳng HI.
95
Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh.
Vẽ bằng ê ke hình vuông ABCD có độ dài cạnh bất kì
Ví dụ 2: Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh bằng 7cm
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 7cm.
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ế ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 7 cm.
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 7 cm.
Bước 4. Vẽ đoạn thẳng CD.
96
Cho lục giác đều ABCDEG. Các đường chéo chính AD, BE, CG cắt nhau tại O ( Hình 9).
Vì sao OA = OB = OC = OD = OE = OG?
Lục giác đều có các đường chéo bằng nhau.
Vì ABCDEG là lục giác đều nên:
Các đường chéo chính bằng nhau và cắt nhau tại O, tạo nên các tam giác đều.
Do vậy, các cạnh OA = OB = OC = OD = OE = OG và bằng nửa độ dài đường chéo chính.
97
Một mảnh vườn có dạng hình vuông với chiều dài cạnh bằng 25m. Người ta để một phần của mảnh vườn làm lối đi rộng 2m như Hình 10, phần còn lại để trồng rau.
a) Tính diện tích phần trồng rau.
b) Người ta làm hàng rào xung quanh mảnh vườn trồng rau và ở một góc vườn rau có để cửa ra vào rộng 2m. Tính độ dài của hàng rào đó.
a) - Tính chiều dài các cạnh của phần trồng rau.
- Công thức diện tích hình vuông dài cạnh a: S = a.a
b) - Tính chu vi vườn rau.
- Độ dài hàng rào bằng chu vi trừ đi độ rộng cửa ra vào.
a)
Phần trồng rau là hình vuông có cạnh là 25-2 = 23 (m)
Diện tích phần trồng rau là:
23 . 23 = 529 (\({m^2}\))
b)
Chu vi vườn rau: 4 . 23 = 92 (m).
Độ dài của hàng rào là:
4 . 23 - 2 = 90 ( m)
Đáp số: a) 529 \({m^2}\).
b) 90 m.
97
Cách gấp và cắt giấy hình tam giác đều, hình lục giác đều từ một mảnh giấy hình vuông
Gấp và cắt theo hướng dẫn
Gấp và cắt như Hình 11 và Hình 12
97
Đố vui: Đố bạn chỉ với 12 que diêm (hay 12 chiếc que có độ dài bằng nhau) mà xếp được thành 6 tam giác đều.
Với 12 que diêm (hay 12 chiếc que có độ dài bằng nhau), ta có thể xếp chúng thành hình lục giác đều với các đường chéo chính cắt nhau, ta được 6 hình tam giác đều.
