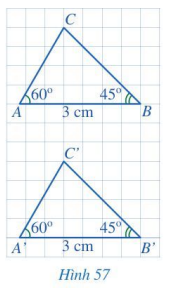
Khởi động
88
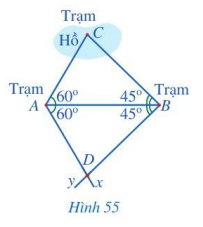
Có ba trạm quan sát A, B, C trong đó trạm quan sát C ở giữa hồ.\(45^o\)
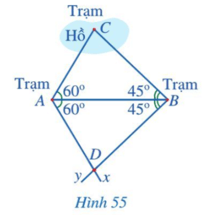
Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được các khoảng cách trên nên người ta làm như sau (Hình 55):
- Đo góc BAC được \(60^o\), đo góc ABC được \(45^o\);
- Kẻ tia Ax sao cho \(\widehat{BAx}\) = \(60^o\) , kẻ tia By sao cho \(\widehat{ABy}\) = \(45^o\), xác định giao điểm D của hai tia đó;
- Đo khoảng cách AD và BD. Ta có AC = AD và BC = BD.
Tại sao lại có hai đẳng thức trên?
Đáp án
Xét ∆ABC và ∆ABD có:
\(\widehat{BAC} = \widehat{BAD} = 60^o\)
AB chung
\(\widehat{ABC} = \widehat{ABD} = 45^o\)
Suy ra ∆ABC = ∆ABD (g - c - g).
Do đó AC = AD (2 cạnh tương ứng) và BC = BD (2 cạnh tương ứng).