Câu hỏi 1
53
Một chiếc xe đi được quãng đường 600 m trong 30 s. Tốc độ của xe là bao nhiêu?
Đáp án
Áp dụng công thức: \( v=\frac{s}{t}=\frac{600}{30}=20(\mathrm{~m} / \mathrm{s})\)
53
Một chiếc xe đi được quãng đường 600 m trong 30 s. Tốc độ của xe là bao nhiêu?
Áp dụng công thức: \( v=\frac{s}{t}=\frac{600}{30}=20(\mathrm{~m} / \mathrm{s})\)
53
Một chiếc xe đang đi với tốc độ 8 m/s.
a. Xe đi được bao xa trong 8 s?
b. Cần bao lâu để xe đi được 160 m?
+Quãng đường chiếc xe đi được trong \(8 \mathrm{~s}\) là: \(\mathrm{s}=\mathrm{v} \cdot \mathrm{t}=8.8=64 \mathrm{~m}\).
+ Thời gian cần thiết để xe đi được \(160 \mathrm{~m}\) là: \(t=\frac{s}{v}=\frac{160}{8}=20 \mathrm{~s}\).
53
Tính tốc độ của chuyển động dựa vào đồ thị quãng đường – thời gian của chuyển động (hình 8.6).
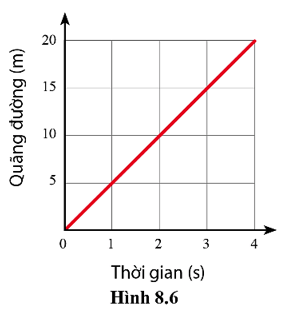

+ Từ đồ thị, tại vị trí \(\mathrm{O}\) của đồ thị kẻ đường vuông góc với trục thời gian tại vị trí 4 s. Cũng từ vị trí đó kẻ đường vuông góc với trục quãng đường tại vị trí 20 m.
\(\Rightarrow\) Vật đi được quãng đường 20 m trong khoảng thời gian 4 s.
+ Áp dụng công thức tính tốc độ của chuyển động: \(v=\frac{s}{t}=\frac{20}{4}=5 \mathrm{~m} / \mathrm{s}\).
53
Trong hình 8.7, đường màu đỏ và đường màu xanh lần lượt biểu diễn đồ thị quãng đường – thời gian của xe A và xe B trong một chuyến đi đường dài.
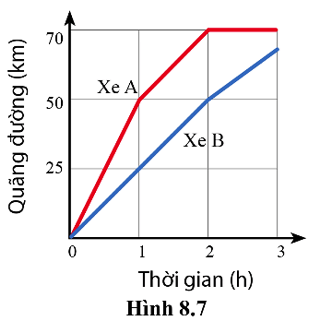
a. Tính quãng đường xe A đi được trong một giờ đầu tiên.
b. Tốc độ của xe A thay đổi như thế nào trong giờ thứ 2 của chuyến đi?
c. Xe B chuyển động nhanh hơn hay chậm hơn xe A trong một giờ đầu tiên?

+ Tại vị trí 1 h trên trục thời gian kẻ đường vuông góc với trục thời gian cắt đồ thị đường màu đỏ (đồ thị của xe A) tại điểm A. Từ điểm \(\mathrm{A}\) kẻ đường vuông góc với trục quãng đường cắt tại vị trí \(50 \mathrm{~km}\). Vậy quãng đường xe \(\mathrm{A}\) đi được trong 1 giờ đầu là \(50 \mathrm{~km}\).
Tốc độ xe A trong 1 giờ đầu: \(v_1=\frac{s_1}{t_1}=\frac{50}{1}=50 \mathrm{~km} / \mathrm{h}\).
+ Tại vị trí \(2 \mathrm{~h}\) trên trục thời gian kẻ đường vuông góc với trục thời gian cắt đồ thị đường màu đỏ (đồ thị của xe \(\mathrm{A}\) ) tại điểm \(\mathrm{C}\). Từ điểm \(\mathrm{C}\) kẻ đường vuông góc với trục quãng đường tại vị trí \(70 \mathrm{~km}\). Vậy quãng đường xe \(\mathrm{A}\) đi trong giờ thứ 2 tương ứng với đoạn đồ thị \(\mathrm{AC}\) là \(\mathrm{s}=70-50=20 \mathrm{~km}\).
Tốc độ xe A đi được trong giờ thứ 2 là: \(v_2=\frac{s_2}{t_2}=\frac{20}{1}=20 \mathrm{~km} / \mathrm{h}\).
Như vậy, ta thấy tốc độ xe \(\mathrm{A}\) đi trong 1 giờ đầu lớn hơn tốc độ xe \(\mathrm{A}\) đi trong giờ thứ 2 là: \(\mathrm{v}_1-\mathrm{v}_2=50-20=30 \mathrm{~km} / \mathrm{h}\).
Vậy tốc độ xe \(\mathrm{A}\) giảm \(30 \mathrm{~km} / \mathrm{h}\) trong giờ thứ 2 của chuyển đi.
+ Tại vị trí \(1 \mathrm{~h}\) trên trục thời gian kẻ đường vuông góc với trục thời gian cắt đồ thị đường màu xanh (đồ thị của xe \(\mathrm{B}\) ) tại điểm \(\mathrm{B}\). Từ điểm \(\mathrm{B}\) kẻ đường vuông góc với trục quãng đường tại vị trí \(25 \mathrm{~km}\). Vậy quãng đường xe \(\mathrm{B}\) đi được trong \(1 \mathrm{~h}\) đầu tiên là \(25 \mathrm{~km}\).
Tốc độ xe \(\mathrm{B}\) đi được trong \(1 \mathrm{~h}\) đầu tiên là: \(v_B=\frac{s}{t}=\frac{25}{1}=25 \mathrm{~km} / \mathrm{h}\).
Khi đó \(\mathrm{v}_{1 \mathrm{~A}}>\mathrm{v}_{1 \mathrm{~B}}\) nên xe \(\mathrm{B}\) chuyển động chậm hơn xe \(\mathrm{A}\) trong một giờ đầu tiên.